Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 4

Plote o ponto cujas coordenadas polares são dadas. Então encontre as coordendas cartesianas do ponto.

a) 2 , 2 π 3 b) 4 ,   3 π c) - 2 ,   - 5 π 6

Passo 1

A questão pede para plotarmos os pontos dados em coordenadas polares. A primeira coordenada fornece o raio e a segunda o ângulo polar.

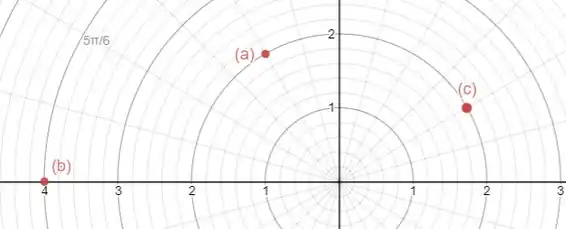
Passo 2

Para achar as coordenadas cartesianas, basta lembrar que

x = r cos ⁡ θ                     e                     y = r   s e n   θ

Assim, para o item (a):

x = 2 cos ⁡ 2 π 3 = 2 ⋅ - 1 2 = - 1                   e                     y = 2   s e n   2 π 3 = 3

Já no item (b):

x = 4 cos ⁡ 3 π = - 4                       e                     y = 4   s e n   3 π = 0      

Por fim, no item (c):

x = - 2 cos ⁡ - 5 π 6 = - 2 ⋅ - 3 2 = 3                 e                   y = - 2   s e n   - 5 π 6 = - 2 ⋅ - 1 2 = 1

Resposta

- 1 ,   3

- 4 ,   0

3 ,   1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 5 , π 6 , 6
O que são coordenadas cilíndricas? Para que tipo de superfícies elas fornecem uma descrição conveniente?
Converta de coordenadas retangulares para coordenadas cilíndricas 3,3 , - 2
Converta de coordenadas retangulares para coordenadas cilíndricas - 1 , - 3 , 2
Converta de coordenadas retangulares para coordenadas cilíndricas 3,4 , 5