Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.2 - Ex. 2
Se
calcule a soma de Riemann com , tomando como pontos amostrais as extremidades à esquerda. (Forneça sua resposta com precisão de seis casas decimais.) O que representa a soma de Riemann? Ilustre com um diagrama.
Passo 1
E aí, galera, belezinha?
O enunciado pede para gente encontrar uma soma de Riemann associada a função
no intervalo e com termos.
Mas você lembra como fazemos uma soma de Riemman 🤔?
Bem, se é uma função e um intervalo contido no domínio de , então a soma de Riemann nesse intervalo é construída desse jeito:
- Escolhemos um número e dividimos o intervalo em intervalos de mesmo comprimento .
- Obtemos os pontos extremos de cada intervalo (), que são dados por
- Escolhemos pontos amostrais em cada intervalo, ou seja, (.
- Obtemos a soma de Riemann dada por
Fica ligado aqui! O enunciado diz pra gente que os pontos amostrais são os pontos esquerdos dos intervalos, ou seja, em cada intervalo escolhemos como ponto amostral o ponto
Então, vamos seguir os passos acima pra resolver essa questão, beleza?
Vamos lá! 😊
Passo 2
Vamos calcular o comprimento de cada intervalo e obter os pontos amostrais associados a cada um deles.
𝐶omo , , e
então temos que
Como os pontos extremos dos intervalos são
então substituindo os valores de , e , temos que
e
Passo 3
Usando as informações obtidas no Passo anterior, vamos calcular a soma de Riemann.
Como , então a soma de Riemann fica:
Fazendo as contas, tem-se que
Passo 4
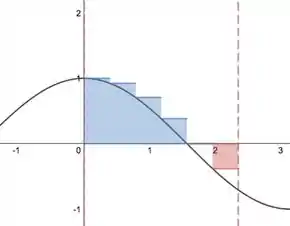
Mas o que será que a soma de Riemann representa? Vamos entender melhor com uma imagem. Podemos visualizar o gráfico da função e o intervalo na figura abaixo.
Este intervalo está dividido em seis partes de mesmo comprimento, e para cada um desses intervalinhos desenhamos um retângulo com altura (que pode ser negativa).
Dessa forma, a soma de Riemann representa a soma das áreas dos quatro retângulos azuis acima do eixo menos a área do retângulo vermelho abaixo do eixo . Note que no quinto intervalo, o valor de é zero, então não tem um retângulo associado.
