Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 83
Ache a medida em radianos do ângulo entre as retas tangentes em cada ponto de intersecao dos gráficos das equações e
Passo 1
Para esse caso, vamos desenhar nossas duas equações:
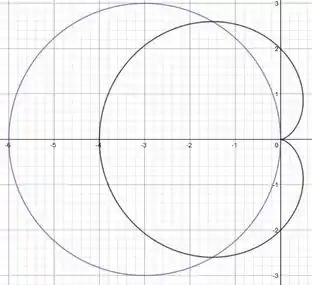
Passo 2
Para as nossas equações, temos 3 pontos de intersecção: A origem e mais dois pontos, que vamos encontrar a seguir.
Logo, = e
Passo 3
Portanto, agora basta fazermos uma subtracao de ângulos:
Resposta
Exercícios de Livros Relacionados
Prove que os gráficos de r= a θ e r θ = a têm um numero ilimitado de pontos de intersecção. Pronve também que as retas tangentes a esses pontos são perpendiculares.
Para a curva r = 2 ( 1 + s e n θ ) , ache X e α no ponto (1, 2 3 π ) . Faça um esboço da curva mostrando X e α .
Para a curva r = 2 cos 1 2 θ ache X e α no ponto (1, 1 6 π ) . Faça um esboço da curva mostrando X e α .
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com