Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 33
- A curvatura da curva mostrada na figura é maior em ou em ? Explique.
- Estime a curvatura em e desenhando o círculo osculador nesses pontos.
Passo 1
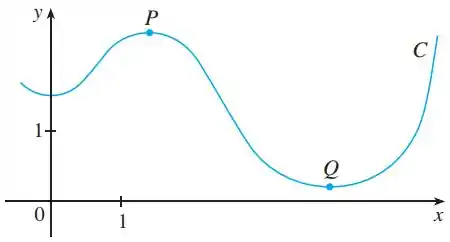
Olá, meu amigo. Vamos analisar a figura:
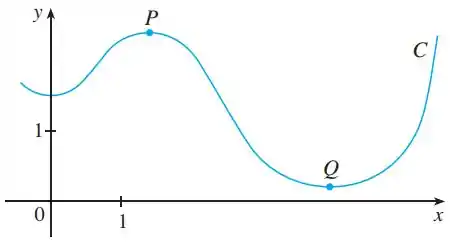
Para respondermos essa atividade.
Por definição: o raio de curvatura é o raio da circunferência osculadora. Então deveremos analisar o raio de curvatura em cada uma e assim teremos uma resposta para a letra a).
Para a letra b) a gente precisa relembrar que um círculo osculador é o círculo que melhor se ajusta a uma curva em um determinado ponto. Esse círculo tem a mesma curvatura e direção que a curva naquele ponto específico, e a sua tangente coincide com a tangente da curva no mesmo ponto. Em outras palavras, é o círculo que "beija" a curva no ponto de contato
Passo 2
- A curvatura é maior em , porque nesse ponto podemos ver que temos uma curva mais fechada em relação ao outro, fazendo com que o vetor tangente mude de direção com uma taxa maior.
- Para estimar a curvatura, basta que saibamos o raio do círculo osculador
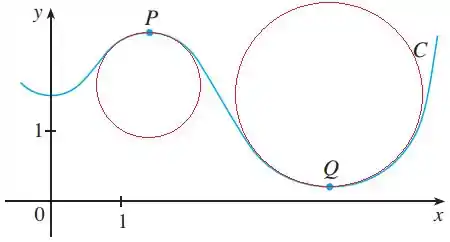
Utilizando a marcação dos eixos como base, visualmente, podemos dizer que o círculo do ponto tem raio de aproximadamente e o círculo do ponto tem raio por volta de , como a curvatura de um círculo é o inverso do seu raio
Resposta
- e