Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.1 - Ex. 28
É dada a área sob o gráfico de e acima do intervalo . Encontre a função e o valor de .
Passo 1
Para encontrarmos a função , devemos derivar a área , uma vez que .
Assim, o gráfico que expressa a função é:
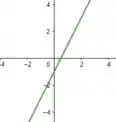
Como a reta é linear do modo , podemos dizer que .
Prontinho!!
Resposta
Exercícios de Livros Relacionados
Use os resultados das Equações 1 e 3 para calcular as integrais nos Exercícios 29-40.29 ∫ 1 2 xd x
Nos Exercícios 23-28, use áreas para calcular as integrais.26 f x = 4 - x 2 , e ma . - 2,2 eb . [ 0,2 ]
Nos Exercícios 23-28, use áreas para calcular as integrais.25 ∫ a b 2 sd s , 0ab