Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 33

  1. Seja

    2. f x = 1 + x 2 1,1 x 2

    Faça um gráfico de f na janela

    - 1,1 × [ 2,5 ; 3,5 ]

    E use sua calculadora para fazer uma conjectura sobre o limite de f x quando x → 0 .

  2. Faça um gráfico de f na janela - 0,001 ; 0,001 × 2,5 ; 3,5

    3. e use sua calculadora para fazer uma conjectura sobre o limite de f x quando x → 0 .

  3. Faça um gráfico de f na janela - 0,00001 ; 0,00001 × [ 2,5 ; 3,5 ]

    4. E use sua calculadora para fazer uma conjectura sobre o limite de f ( x ) quando x → 0 .

  4. Mais adiante, teremos condições de mostrar que

lim x → 0 ⁡ 1 + x 2 1,1 x 2 ≈ 3,00416602

Qual é o defeito que os gráficos obtidos nos itens anteriores revelam sobre o uso de evidência numérica para fazer conjecturas sobre limites?

Passo 1

E aí, tudo joia?

Vamos dar uma olhada nesses gráficos! A gente vai adaptar a janela do Geogebra pra ficar nesses intervalos aí, ok?

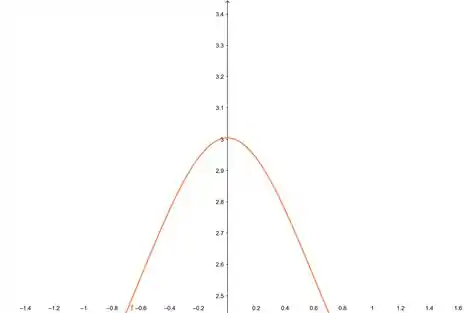
  1. Aqui é no intervalo de - 1,1 × 2,5 ; 3,5 , lembrando que é eixo x × eixo y :

    2. Usando o próprio programa pra calcular o limite, constamos que nesse caso o limite da função é:

    lim x → 0 ⁡ 1 + x 2 1,1 x 2 = 3

    Passo 2

  2. Vamos diminuir esse intervalo para - 0,001 ; 0,001 × 2,5 ; 3,5 . Olha o gráfico:

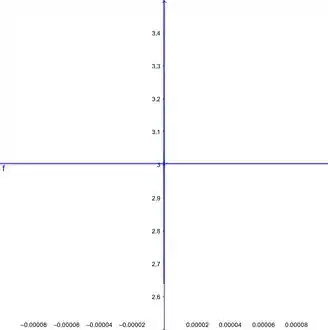
    3. Bem estranho né? Mas de novo, aqui quando x = 0 o limite parece ser 3.

    Passo 3

  3. Fazendo esse intervalo mais minucioso ainda...

    4. Aqui já deu essa embolada de pontos ali onde x = 0 , então por essa imagem, a gente falaria que o limite em x = 0 não existe.

    Passo 4

  4. Bom, os gráficos apresentam aproximações, e não exatidão. Sendo assim, ao olharmos um gráfico concluímos algo sobre uma função que nem sempre é verdade. Porém são ótimos recursos para auxiliar o estudo!

Resposta

  1. 3.
  2. 3.
  3. Não existe.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dado f x = L . Determine um número δ para o ε dado tal que f x - L ε sempre que 0x - aδ . Dar exemplos de dois outros números positivos para δ , que também satisfazem a implicação dada. x 2 - 4 x +
É dado f x = L . Determine um número δ para o ε dado tal que f x - L ε sempre que 0x - aδ . Dar exemplos de dois outros números positivos para δ , que também satisfazem a implicação dada. = 2 , ε = 0,
Faça o gráfico das funções y = f ( x ) dadas, explorando escalar para visualizar melhor o gráfico numa vizinhança da origem. Observando o gráfico, qual a sua conjectura sobre o lim x → 0 ⁡ f ( x ) ? C
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 2 ⁡ x + 4 3 x - 1
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → - 1 [ ⁡ x + 4 3 × x + 2 - 1 ]