Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 27
Nos Exercícios 23-28, use áreas para calcular as integrais.
26
Passo 1
O enunciado pede para gente calcular o valor dessa integral usando o valor da área em baixo da curva da função.
Passo 2
A função é dada por
Isso vai dar o seguinte gráfico
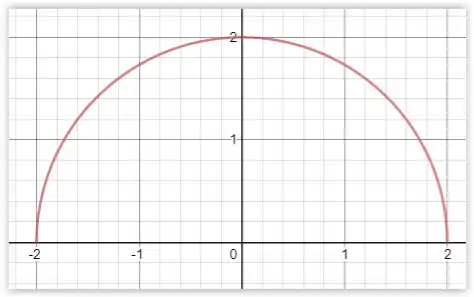
Passo 3
Repare que o gráfico vai formar um semicírculo, e para calcular a área do semicírculo usamos
Repare que o raio vale 2
Passo 4
No item b, repare que a área em baixo da figura será exatamente a metade da do item a
Então teremos o seguinte
Por tanto
Resposta
O resultado da integral é no item a, e no item b.
Exercícios de Livros Relacionados
Nos exercícios de 1 a 10 , calcular a integral e, em seguida, derivar as respostas para conferir os resultados. ∫ x 3 x d x
Nos exercícios de 1 a 10 , calcular a integral e, em seguida, derivar as respostas para conferir os resultados. ∫ d x s e n 2 x
Nos exercícios de 1 a 10 , calcular a integral e, em seguida, derivar as respostas para conferir os resultados. ∫ 2 x 2 - 3 2 d x
Nos exercícios de 1 a 10 , calcular a integral e, em seguida, derivar as respostas para conferir os resultados. ∫ x 5 + 2 x 2 - 1 x 4 d x
Nos exercícios de 1 a 10 , calcular a integral e, em seguida, derivar as respostas para conferir os resultados. ∫ 9 t 2 + 1 t 3 d t