Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 21a
21. Dada . (a) Prove que é contínua à direita de 4. (b) Prove que não existe. (c) Faça um esboço do gráfico de
Letra (a)
Passo 1
O enunciado pede para provarmos que f(x) é contínua à direita de 4, ou seja, para x > 4. Vale lembrar também que uma função é contínua lateralmente em um ponto se o limite lateral coincidir com o valor da função no ponto em questão.
Passo 2
Para mostrar que ela é contínua à direita de 4, basta mostrar que o limite lateral à direita de 4 é igual a f(4). Entao, temos :
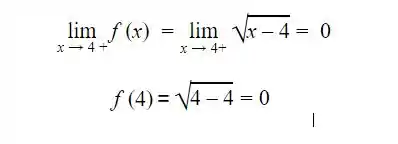
Passo 3
Portanto,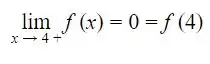 
. Logo, f é contínua à direita nesse ponto.
Resposta
Demonstração.
Exercícios de Livros Relacionados
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
Os gráficos de uma função f e sua derivada f ' são mostrando. Qual é maior, f ' ( - 1 ) ou f ' ' ( 1 ) ?
O gráfico de f é dado. Declare, com razões, os números em que f não é diferenciável.
Calcular a diferencial das seguintes funções:(a) y = ln ( 3 x 2 - 4 x ) ;(b) y = x + 1 e x ;(c) y = sin ( 5 x 2 + 6 )