Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 42
O gráfico de é dado. Declare, com razões, os números em que não é diferenciável.
Passo 1
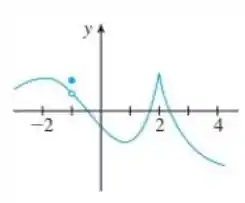
E aí, tudo bom?! Esse problema é direto e reto, temos o gráfico:
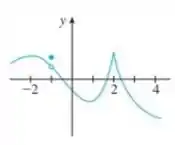
Aqui a gente quer saber em quais pontos a função acima não é diferenciável!
Na prática, pra uma função ser diferenciável em um ponto deve ser contínua nesse ponto, mas quando a curva tem uma mudança abrupta, como uma “quina” ou uma “dobra” , ou então um ponto de inflexão, ela não vai ser derivável!
Isso porque a derivada é a inclinação da reta tangente a curva no ponto, maaas se a gente tem uma quina, ou então um ponto de inflexão a sua reta tangente vai ser vertical. E qual é a inclinação de uma reta vertical?!
Seria infinito, certo?! Se não é um número então dizemos que a função não é diferenciável nesse caso!
Agora vamos ao que interessa, mãos à obra!
Passo 2
Vamos trazer o gráfico pra pertinho:
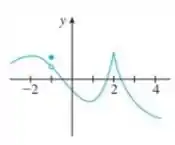
Bom galera, observando bem o gráfico a gente nota que temos valores de com pontos interessantes na função:
- Uma descontinuidade;
- Um ponto de bico.
Beleza, como uma função não é derivável em uma desconuidade, nem em um ponto de bico, então a função não é diferenciável nesses pontos:
Prontinho!