Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 47
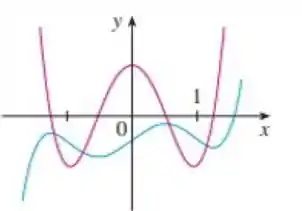
Os gráficos de uma função e sua derivada são mostrando. Qual é maior, ou ?
Passo 1
Opaa, não precisa assustar com essa questão não. Vem comigo que nós vamos destruir esse problema apenas analisando o gráfico, vamos lá!!
Temos o seguinte problema! O enunciado nos dá:
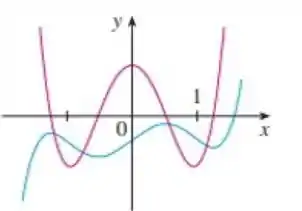
Uma curva representa a função e outro sua derivada . A partir dessas funções, precisamos determinar qual é o maior entre e .
O enunciado não deixa claro qual curva é qual mas podemos perceber que toda vez o gráfico azul chega em um topo ou em um mínimo o gráfico vermelho está em . Sabendo que a derivada de uma constante é . Então podemos concluir que o gráfico vermelho é a derivada do azul, logo:
Gráfico azul
E
Gráfico vermelho
Passo 2
Agora temos que responder qual número é maior ou !
Pra responder esse problema iremos observar o gráfico:
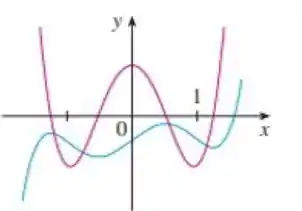
Beleza, agora olha que em que é o gráfico vermelho, tem mínimo locais quando e , com isso a gente tem que:
E como é negativo, ou seja é menor que , dessa forma . Graficamente, isso significa que a concavidade da função de é maior do que a inclinação de função , indicando uma mudança na direção da curvatura da função original nesse ponto.
Prontinho!