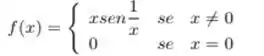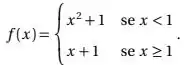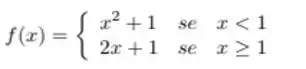Exercícios de Diferenciabilidade - Lista de Exercícios Resolvida
Questão 1
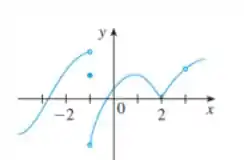
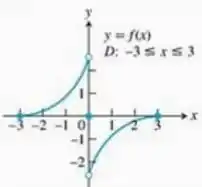
No exercício, cada figura mostra o gráfico de uma função em um intervalo fechado . Em que pontos do domínio a função parece ser
derivável?
contínua, mas não derivável?
nem contínua nem derivável?
Justifique sua resposta.
Questão 2
Considere a função definida por:
Dê um exemplo de valores para e tal que exista , porém não seja contínua em
Determine e de forma que seja contínua em
Para os valores de e obtidos no item anterior, existe ?
Ver solução completaQuestão 3
Seja
Calcule, se existir, . Justifique sua resposta.
A função é diferenciável em ?
Ver solução completaQuestão 9
Seja
Calcule, se existir, . Justifique sua resposta.
A função é diferenciável em ?
Ver solução completaQuestão 10
Considere a função
Esboce o gráfico de .
Determine analiticamente o(s) ponto(s) em que é descontínua.
Esta(s) descontinuidade(s) pode(m) ser removida(s)? Justifique.
A função é diferenciável em ? Justifique.
Ver solução completaQuestão 13
15. Dada a função ,
a) Determine um valor de para o qual é contínua em ;
Ver solução completaQuestão 14
Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.
- Se é derivável até segunda ordem com e , para todo , então
Questão 15
15. Dada a função ,
b) é derivável no ponto encontrado no item anterior?
Ver solução completaQuestão 16
Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.
- Se então
Questão 17
Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.
d) se existe uma assíntota para (quando ) com coeficiente angular e se existe , então
Ver solução completaQuestão 18
Sejam e funções reais a valores reais. Considere as seguintes afirmações:
- Se é contínua em , então é derivável em .
- Suponha inversível com inversa , derivável em , contínua em e . Então é derivável em .
- Se e forem ambas descontínuas em , então é descontínua em .
São verdadeiras:
- Apenas a afirmação I
- Apenas a afirmação II
- Apenas a afirmação III
- Todas as afirmações
- Apenas as afirmações II e III
Questão 21
Assinale a alternativa cuja afirmação é verdadeira
- Se é uma função derivável, com derivada contínua, tal que possui pontos críticos, então possui extremos locais.
- Se é uma função qualquer tal que , então existe tal que
- Se é uma função derivável, com derivada contínua, é o único ponto crítico de e é o ponto de mínimo local de então é o ponto de mínimo global de .
- Se é uma função contínua tal que é derivável em e , então existe tal que
- Se é uma função derivável tal que e para todo , então para todo
Questão 22
Assinale a alternativa cuja afirmação é verdadeira
- Se é uma função derivável tal que não possui pontos críticos, então não possui extremos globais
- Se é uma função qualquer tal que , então existe tal que
- Se é uma função contínua tal que é derivável em e , então existe tal que
- Se é uma função derivável e é o único ponto crítico de , então é extremo global de .
- Se é uma função derivável tal que e para todo , então para todo
Questão 23
Seja , .
(a) Dê os pontos onde é duas vezes diferenciável e determine e .
Ver solução completaQuestão 26
Sejam e números reais tais que a função
É diferenciável em toda parte. O valor de é
(A) 38
(B) 37
(C) 39
(D) 40
(E) 36
Ver solução completaQuestão 27
Questão 3:
Sejam . Considere a função definida por
onde
- Determine os valores de e para que a função seja contínua e diferenciável.
- Esboce abaixo o gráfico de . Desenhe também a reta tangente ao gráfico de no ponto
Questão 28
Considere a função dada por:
(c) Sejam e considere a função dada por:
Determine os valores de e para que a função seja contínua e diferenciável.
Ver solução completaQuestão 29
(Stewart) Usando um aplicativo para construir gráficos de funções, dê zoom em direção aos pontos , e sobre o gráfico da função . O que você observa? Explique o que você viu em termos da diferenciabilidade da função .
Ver solução completaQuestão 31
Usando a definição de derivada, encontre a inclinação da reta tangente ao gráfico das funções abaixo, nos pontos indicados:
b); .
Ver solução completaQuestão 32
Usando a definição de derivada, encontre a inclinação da reta tangente ao gráfico das funções abaixo, nos pontos indicados:
c); .
Ver solução completaQuestão 33
Considere as funções
e
(g) Indique nos gráficos os pontos em que , e não são diferenciáveis
Ver solução completaQuestão 34
Usando a definição de derivada, encontre a inclinação da reta tangente ao gráfico das funções abaixo, nos pontos indicados:
d); .
Ver solução completaQuestão 35
Usando a definição de derivada, encontre a inclinação da reta tangente ao gráfico das funções abaixo, nos pontos indicados:
- ; .
Questão 37
Considere , com uma função duas vezes diferenciável. Então, a função é duas vezes diferenciável e satisfaz:
Ver solução completaQuestão 44
Assinale (VERDADEIRO) ou F (FALSO). Se VERDADEIRO, justifique sua resposta, se FALSO, apresente uma função que satisfaça tal propriedade.
() Se for uma função contínua no ponto , então é derivável em .
() Se for uma função derivável no ponto , então é contínua em .
() Se existe, então .
Ver solução completaQuestão 45
Determine a e b reais para que a função f dada por seja derivável em 1.
Ver solução completaQuestão 46
Se é uma função diferenciável tal que e em .
b) Prove que existem e em tais que
Ver solução completaQuestão 49
Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.
e) se , então tem uma assíntota com coeficiente angular igual a
Ver solução completaQuestão 52
Se para e para , determine se existem tais que seja diferenciável em .
Ver solução completaQuestão 53
3. Uma função satisfaz as seguintes propriedades:
- e
- é estritamente crescente em e
- é uma função par
c. é derivável no ponto ? Justifique.
Ver solução completaQuestão 57
Determine, se existirem, os valores de para que a função
Seja derivável em .
Ver solução completaQuestão 58
Seja dada por
(a) A função é contínua em ? Justifique sua resposta.
(b) A função é derivável em ? Justifique sua resposta. Caso sim, encontre a equação da reta tangente ao gráfico de em .
Ver solução completaQuestão 59
(Stewart) Usando um aplicativo para construir gráficos de funções, faça o gráfico da função . Dê zoom primeiro em direção ao ponto e, então, em direção à origem. Qual a diferença entre os comportamentos de próximo a esses dois pontos? O que você conclui sobre a diferenciabilidade de ?
Ver solução completaQuestão 60
Seja
- Determine se é contínua no ponto ).
- Determine se é diferenciável no ponto (0,0).
Questão 61
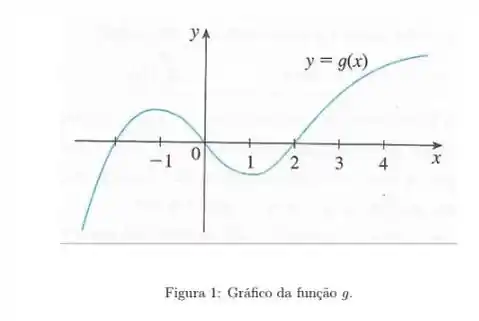
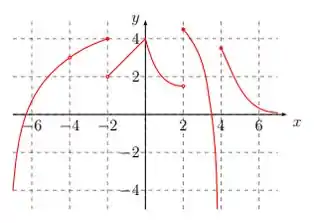
- Considere a função cujo gráfico está representado abaixo. Determine os pontos em que não é diferenciável.
Questão 62
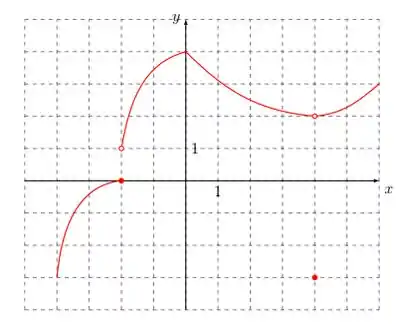
- Considere a função cujo gráfico está representado abaixo. Determine os pontos no intervalo em que não é diferenciável.
Questão 63
Parte 1: Mostre que é derivável em e calcule
Parte 2: Esboce o gráfico de
Ver solução completaQuestão 64
5. Mostre que a função não é diferenciável em . Encontre uma fórmula para e esboce seu gráfico.
Ver solução completaQuestão 65
Seja . Verifique se é contínua e diferenciável em . Esboce o gráfico de .
Ver solução completaQuestão 66
Um balão meteorológico é solto e sobe verticalmente de modo que sua distância do solo durante os primeiros segundos de voo é dada por , na qual é contada em metros e em segundos. Determine a velocidade do balão no instante em que o balão está a metros do solo.
Ver solução completaQuestão 67
Decida se a proposição abaixo é falsa ou verdadeira, justificando:
Se não é derivável em , então
Ver solução completaQuestão 68
Seja . Verifique se é contínua e diferenciável em . Esboce o gráfico de .
Ver solução completaQuestão 70
Parte 1: Mostre que não é derivável em e calcule
Parte 2: Esboce o gráfico de
Ver solução completaQuestão 72
Suponha que f é uma função derivável em = 0 e que f(0) = 0. Mostre que para alguma função g que é contínua em = 0.
Dica: O que acontece se você tentar escrever ?
Ver solução completaQuestão 73
Seja f uma função derivável em e considere a função . Calcule e . Interprete geometricamente os resultados obtidos.
Ver solução completaQuestão 76
(10) (a) Prove que se é diferenciável em , então também é diferenciável em desde que .
Ver solução completaQuestão 78
- Considere a função dada por
- Mostre que se é diferenciável em e calcule
- Usando o fato que é diferenciavel em todos os pontos de , calcule para cada e mostre que a função não é continua em .
Questão 80
5. Considere a função dada por
Determine para que seja diferenciável em .
Ver solução completaQuestão 82
Seja uma função diferenciável num intervalo . Considere a função .
(a) é contínua em ? Justifique.
Ver solução completaQuestão 84
Sejam f : R → R derivável em = 0 tal que f(0) = f ′ (0) = 0 e g : R → R uma função limitada (não necessariamente derivável em x0 = 0). A função h(x) = f(x)g(x) é derivável em = 0? Exiba h ′ (0) em caso afirmativo
Ver solução completaQuestão 85
Responda, justificando:
a. Se f + g é derivável em , é verdade que f e g são necessariamente deriváveis em ?
b. Se f · g é derivável em , quais condições sobre f garantem a derivabilidade de g em ?
Ver solução completaQuestão 86
Prove que:
a. Se f é derivável em , então | f(x)| é derivável em , desde que f() ≠0. Dê um contra-exemplo no caso em que f() = 0.
b. Não é possível escrever x = f(x)g(x) com f , g deriváveis tais que f(0) = g(0) = 0
Ver solução completaQuestão 88
Verifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaQuestão 89
Verifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaQuestão 90
Verifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaQuestão 91
Sejam e funções deriváveis em um intervalo aberto e
Mostre que é derivável em se e somente se e . Construa contraexemplos removendo uma das condições de cada vez
Ver solução completaQuestão 92
Verifique se cada uma das funções abaixo é contínua e se é derivável no ponto indicado.
Ver solução completaQuestão 93
Mostre que se é derivável em e,
então o coeficiente angular da reta normal ao gráfico de em é
Ver solução completaQuestão 94
- Estude, em função dos valores , a continuidade da função dada por
- Analise a diferenciabilidade de em para os casos de e .
Ver solução completaQuestão 95
5. Calcule , onde é a circunferência , percorrida no sentido positivo, e é a circunferência ; percorrida no sentido horário.
Ver solução completaQuestão 98
Assinale a única alternativa correta sobre a função dada por
- Ela é uma função inteira
- Ela não é derivável em nenhum ponto
- Ela é derivável apenas em z = 0
- Ela é derivável na circunferência dada por |Z| = 1
- Ela é analítica em z = 0
Questão 99
Seja uma função diferenciável num intervalo . Considere a função .
(b) Determine o valor de para que seja diferenciável em . Justifique.
Ver solução completaQuestão 101
Seja a função
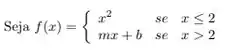
Escolha os valores de e que tornam a função derivável em todo lugar
Ver solução completaQuestão 105
Decida, justificando ou apresentando contra-exemplo, se cada uma das sentenças abaixo é verdadeira ou falsa:
a. Se f é derivável em , então | f(x)| é derivável em , desde que f() ≠0. E no caso em que f() = 0?
b. Se f, g são duas funções deriváveis em , então as funções e são deriváveis em ;
c. Suponha , onde g é uma função contínua em = 0. Então f é derivável em = 0. Se for verdadeira, calcule f ′ (0) em termos de g;
d. É possível escrever x = f(x)g(x) com f , g deriváveis tais que f(0) = g(0) = 0.
Ver solução completaQuestão 106
3. Seja a funçã cujo gráfico está abaixo.
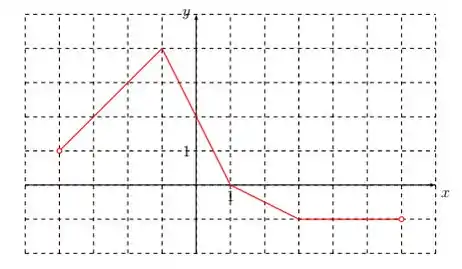
- Em quais pontos do domínio não é contínua?
- Em quais pontos do domínio não é diferenciavel?
- Represente graficamente .
Questão 107
Sejam cujos gráficos são:
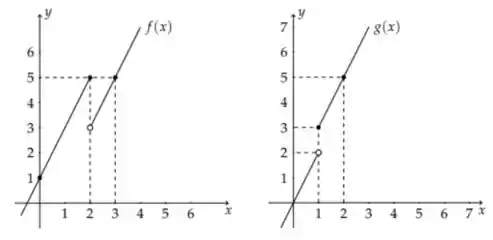
Então pode-se dizer que :
a) não é derivável somente em ;
b) não é derivável somente em ;
c) não é derivável somente em e ;
d) é derivável em todos os pontos e ;
e) é derivável em todos os pontos e .
Ver solução completaQuestão 108
Prove que se f e g são diferenciaveis em a, então as funções max(f, g) e min(f, g)
são diferenciaveis em a desde que .
Ver solução completaQuestão 111
Considere
b. Determine uma curva , derivável e cuja imagem seja igual ao gráfico de .
Ver solução completaQuestão 112
Considere
c. Interprete geometricamente o fato de que f não é derivável em x = 0, mas a curva γ é derivável em , onde .
Ver solução completaQuestão 114
Decida se cada função a seguir é ou não diferenciável na origem. Justifique!
Ver solução completaQuestão 115
Decida se cada função a seguir é ou não diferenciável na origem. Justifique!
Ver solução completaQuestão 116
Sejam derivável e tais que . Determine qual das
alternativas abaixo implica a existência de um c entre tal que
Ver solução completaQuestão 117
Seja uma função derivável e seja fixado. Verifique as afirmações são verdadeiras ou falsas. Justifique.
- Se , para todo , então
Questão 118
Se é uma função diferenciável tal que e em .
e) Utilizando o item b), se e , calcule e .
Ver solução completaQuestão 119
Considere a função
c) é uma função diferenciável em todo seu domínio?
Ver solução completaQuestão 120
(2) Encontre o volume comum de dois cilindros circulares, cada um com raio , se os eixos dos cilindros se intersectam em ângulos retos.
Ver solução completaQuestão 122
Considere a função abaixo:
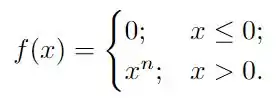
Onde é um número inteiro positivo. Para que valores de a função é derivável em ? Para que valores de a função é contínua em ?
Ver solução completa