Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 75

Dada a tabela a seguir, encontre as derivadas indicadas em (a) e (b)

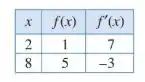
  1. g ' 2 , onde g x = f x 3 .
  2. h ' 2 , onde h x = f x 3 .

Passo 1

  1. Vamos começar calculando g ' x . Note que para fazer isso, devemos usar a regra da cadeia, pois temos uma composição de funções. Note:

    2. f x 3 = u f x

    onde u x = x 3 . Assim,

    d d x f x 3 = f ' x   u ' f x d d x f x 3 = f ' x ⋅ 3 f x 2 d d x f x 3 = 3 f ' x f x 2

    Portanto, fazendo x = 2 , temos

    g ' 2 = 3 ⋅ f ' 2 ⋅ f 2 2 g ' 2 = 3 ⋅ 7 ⋅ 1 2 g ' 2 = 21 .

    Passo 2

  2. Note que temos novamente uma composição de funções. Veja:

f x 3 = f v x

onde v x = x 3 . Logo,

d d x f x 3 = v ' x   f ' v x d d x f x 3 = 3 x 2   f ' x 3

Sendo assim,

h ' 2 = 3 ⋅ 2 2 ⋅ f ' 2 3 h ' 2 = 12 ⋅ - 3 h ' 2 = - 36

Resposta

  1. 21 .
  2. - 36 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados y = f ( u ) e u = g ( x ) , determine d y d x = f ' g x g ' x y = 6 u - 9 u = 1 2 x 4
Dados y = f ( u ) e u = g ( x ) , determine d y d x = f ' g x g ' x y = s e n ( u ) u = x - cos ⁡ x
Dados y = f ( u ) e u = g ( x ) , determine d y d x = f ' g x g ' x y = t g ( u ) u = 10 x - 5
Dados y = f ( u ) e u = g ( x ) , determine d y d x = f ' g x g ' x y = cos ⁡ u u = - x / 3
Dados y = f ( u ) e u = g ( x ) , determine d y d x = f ' g x g ' x y = 2 u 3 u = 8 x - 1