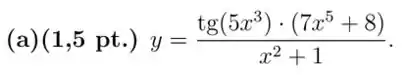Exercícios de Regra da Cadeia - Lista de Exercícios Resolvida
Questão 4
Derive a seguinte função (se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 7
Seja uma função diferenciável tal que e . Considere a função
Calcule .
Ver solução completaQuestão 9
Utilizando as regras de derivação, calcule a derivada das seguintes funçōes:
b)
Ver solução completaQuestão 11
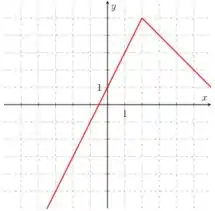
Seja a função definida por
Determine os pontos em que é derivável. Justifique.
Calcule nos pontos em que é derivável.
Ver solução completaQuestão 31
Calcule ou argumente que os valores não existem. Em todos os casos justifique seus cálculos e respostas.
Derivada de .
Ver solução completaQuestão 33
Calcule a derivada das seguintes funções, usando as regras de derivação:
Ver solução completa
Questão 34
Calcule a derivada das seguintes funções, usando as regras de derivação:
Calcule para
Ver solução completaQuestão 40
Derive as funções dos exercícios 6 a 16 (se for conveniente, use derivação logarítmica)
6)
Ver solução completaQuestão 41
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
9)
Ver solução completaQuestão 42
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
14)
Ver solução completaQuestão 43
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
7)
Ver solução completaQuestão 44
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
8)
Ver solução completaQuestão 45
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
12)
Ver solução completaQuestão 46
Derive as funções dos exercícios a (se for conveniente, use derivação logarítmica)
16)
Ver solução completaQuestão 47
(3) (a) Um objeto circular aumenta de tamanho de uma forma não especificada, mas sabe-se que quando o raio é , a sua taxa de variação é . Encontre a taxa de variação da área quando o raio é .
Ver solução completaQuestão 52
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Ver solução completaQuestão 54
Derive cada função (se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 69
18. Considere uma função diferenciável e definida por . Sabendo que e , calcule .
Ver solução completaQuestão 74
Considere duas funções e . Sabemos que , , , , , e .
Se = , então o valor de é:
Questão 83
Determine a derivada da função
(a)
(b)
(c)
(d)
(e) Nenhuma das respostas anteriores
Ver solução completaQuestão 84
Considere uma função diferenciável e definida por . Sabendo que , calcule
Ver solução completaQuestão 91
A equação de movimento de um objeto é dada por e em metros e em segundos.
- Determine a velocidade em m/s
- Determine a aceleração em m²/s
- Determine a aceleração no
- Determine a aceleração no(s) instante(s) em que a velocidade é igual a 0
Questão 92
Determine a diferencial das funções abaixo, com os valores de e indicados
Questão 98
A composição de funções tem uma interpretação mais natural em contextos aplicados. Por exemplo, imagine um objeto de massa movendo-se sobre uma linha reta com velocidade em função do tempo dada por. Sabemos que a energia cinética deste objeto, em termos da velocidade, é dada por. Uma pergunta natural aqui seria determinar a energia cinética em função do tempo. Isso é fácil de fazer, basta substituir o valor de , isto ,. Apesar de não parecer, fizemos uma composição de funções aqui. Traduzindo para o contexto matemático, pensemos que as duas funções envolvidas (escritas na variável x) são e .
A composição de com tem como resultado que é o mesmo resultado obtido acima, apenas com o nome da variável diferente. Essa interpretação é útil para analisarmos a regra da cadeia sob um outro ponto de vista. Nesse exemplo, e .
Curiosamente, a derivada da composição pode ser vista como
Você pode dizer prontamente que isso não dá a mesma coisa que usar a regra da cadeia. Lembremos que , na verdade, tem uma escrita em termos de . Substituindo, obtemos que é a resposta dada pela regra da cadeia. Em resumo, a regra da cadeia escrita da forma (última linha da tabela no início da lista) está correta, entendendo que o termo será escrito em termos de após substituir .
Em cada item, determine o que se pede.
(b) Dados , onde e são constantes em e , determine .
Sugestão: Faça a questão acima por três métodos diferentes: (1) escrevendo as funções com o mesmo nome de variável e aplicando a regra da cadeia padrão; (2) Substituindo a segunda função dentro da primeira e já trabalhando com a primeira função na variável sobre a qual queremos derivar e (3) usando a fórmula , obtendo uma escrita híbrida com e , e depois substituir pelo seu valor em termos de .
Ver solução completaQuestão 99
A composição de funções tem uma interpretação mais natural em contextos aplicados. Por exemplo, imagine um objeto de massa movendo-se sobre uma linha reta com velocidade em função do tempo dada por. Sabemos que a energia cinética deste objeto, em termos da velocidade, é dada por. Uma pergunta natural aqui seria determinar a energia cinética em função do tempo. Isso é fácil de fazer, basta substituir o valor de , isto , . Apesar de não parecer, fizemos uma composição de funções aqui. Traduzindo para o contexto matemático, pensemos que as duas funções envolvidas (escritas na variável x) são e .
A composição de com tem como resultado que é o mesmo resultado obtido acima, apenas com o nome da variável diferente. Essa interpretação é útil para analisarmos a regra da cadeia sob um outro ponto de vista. Nesse exemplo, e .
Curiosamente, a derivada da composição pode ser vista como
Você pode dizer prontamente que isso não dá a mesma coisa que usar a regra da cadeia. Lembremos que , na verdade, tem uma escrita em termos de . Substituindo, obtemos que é a resposta dada pela regra da cadeia. Em resumo, a regra da cadeia escrita da forma (última linha da tabela no início da lista) está correta, entendendo que o termo será escrito em termos de após substituir .
Em cada item, determine o que se pede.
(c) Dados , onde é constante em e , determine .
Sugestão: Faça a questão acima por três métodos diferentes: (1) escrevendo as funções com o mesmo nome de variável e aplicando a regra da cadeia padrão; (2) Substituindo a segunda função dentro da primeira e já trabalhando com a primeira função na variável sobre a qual queremos derivar e (3) usando a fórmula , obtendo uma escrita híbrida com e , e depois substituir pelo seu valor em termos de .
Ver solução completaQuestão 100
A composição de funções tem uma interpretação mais natural em contextos aplicados. Por exemplo, imagine um objeto de massa movendo-se sobre uma linha reta com velocidade em função do tempo dada por . Sabemos que a energia cinética deste objeto, em termos da velocidade, é dada por. Uma pergunta natural aqui seria determinar a energia cinética em função do tempo. Isso é fácil de fazer, basta substituir o valor de , isto , . Apesar de não parecer, fizemos uma composição de funções aqui. Traduzindo para o contexto matemático, pensemos que as duas funções envolvidas (escritas na variável x) são e .
A composição de com tem como resultado que é o mesmo resultado obtido acima, apenas com o nome da variável diferente. Essa interpretação é útil para analisarmos a regra da cadeia sob um outro ponto de vista. Nesse exemplo, e .
Curiosamente, a derivada da composição pode ser vista como
Você pode dizer prontamente que isso não dá a mesma coisa que usar a regra da cadeia. Lembremos que , na verdade, tem uma escrita em termos de . Substituindo, obtemos que é a resposta dada pela regra da cadeia. Em resumo, a regra da cadeia escrita da forma (última linha da tabela no início da lista) está correta, entendendo que o termo será escrito em termos de após substituir .
Em cada item, determine o que se pede.
(a) Dados onde é constante em e , determine .
Sugestão: Faça a questão acima por três métodos diferentes: (1) escrevendo as funções com o mesmo nome de variável e aplicando a regra da cadeia padrão; (2) Substituindo a segunda função dentro da primeira e já trabalhando com a primeira função na variável sobre a qual queremos derivar e (3) usando a fórmula , obtendo uma escrita híbrida com e , e depois substituir pelo seu valor em termos de .
Ver solução completaQuestão 101
A posição de uma partícula sobre uma corda vibrante é dada pela equação , em que é medido em centímetros e em segundos. Determine a função velocidade da partíula.
Ver solução completaQuestão 110
O deslocamento de uma partícula em uma corda vibrante é dado pela equação onde s é medido em centímetros e , em segundos. Encontre a velocidade da partícula após segundos.
Ver solução completaQuestão 111
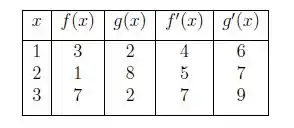
Considere as funções dadas por e e os valores dados na tabela abaixo, encontre:
Questão 116
A Lei de Gravitação de Newton diz que a intensidade da força exercida por um corpo de massa sobre um corpo de massa é
Em que é a constante gravitacional e é a distância entre os corpos. Calcule e explique seu significado. O que o sinal de menos indica?
Ver solução completaQuestão 117
A posição de uma partícula sobre uma linha reta graduada em metros no instante segundos é dada por
- Determine
- Determine
- Em quais instantes a partícula está em repouso?
- Quando a partícula está se movendo para frente? E quando está se movendo para trás?
- Qual é o deslocamento da partícula entre os instantes e ?
- Qual é a distância percorrida pela partícula entre os instantes 0 e 5s?
- Para que valores de tem-se Para quais valores de tem-se Para quais valores de tem-se
- Quando a partícula está acelerando ou freando?
Questão 118
A quantidade de carga , em coulombs (C), que passa através de um ponto em um fio até o instante (medido em segundos) é dada por
Em que e são constantes. Determina a corrente neste ponto do fio no instante t. Quais são as unidades de medida?
Ver solução completaQuestão 129
A função secante , como o domínio restrito e contradomínio restrito ao intervalo , é bijetiva sendo portanto invertível. Sua inversa é definida por
Sabendo que ela é derivável em , siga os passos abaixo para calcular
- Use a regra do quociente (ou a da cadeia) para mostrar que
- Aplique o operador de derivação em ambos da igualdade de não esquecendo de usar a regra da cadeia para derivar o lado direito da igualdade
- Isole o termo na expressão encontrada acima
- Lembrando que e , escreva como função de x
- Substitua e na sua resposta do item c) para obter a expressão como função apenas da variável x
Questão 133
Seja uma função duas vezes diferenciável. Considere:
Então , onde
- .
- .
- .
- .
- .
Questão 134
Sejam , : funções diferenciáveis tais que:
Então a derivada da função no ponto é:
- .
- .
- .
- .
- .
Questão 143
Questão 2) Calcule a derivada das seguintes funções, usando as regras de derivação:
c)
Ver solução completaQuestão 145
Questão 3:
Use a regra de derivação e calcule a função derivada em cada caso.
c)
Ver solução completaQuestão 148
O deslocamento de uma partícula sobre uma corda vibrante é dado pela equação
Em quais instantes de tempo a partícula está parada?
Ver solução completaQuestão 149
Cristais de clorato de sódio são fáceis de crescer no formato de cubos permitindo uma solução de água e clorato de sódio evaporar vagarosamente. Se for o volume de cada cubo com comprimento de lado :
Calcule quando e explique seu signficiado.
Ver solução completaQuestão 152
Uma escada com 10m de comprimento está apoiada numa parede vertical. Seja o ângulo entre o topo da escala e a parede e a distância da base da escada até a parede. Se a base da escada escorregar para longe da parede, com que rapidez variará em relação a quando ?
Ver solução completaQuestão 163
22. Determine e reais para que as curvas e sejam tangentes no ponto .
Ver solução completaQuestão 166
A quantidade de carga em coulombs (C) que passa através de uma seção reta de um fio até
o instante (medido em segundos) é dada por
Calcule a primeira derivada da função
Encontre em que instante a corrente é mais baixa
Ver solução completaQuestão 171
Em várias situações precisamos encontrar uma forma de calcular a derivada da função composta a partir das derivadas das funções componentes, assim podemos aplicar a regra da cadeia: Sejam e duas funções deriváveis, com e consideremos a função composta . Então é derivável e , para todo
Aplicando então a regra da cadeia calcule a derivada de
Ver solução completaQuestão 177
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Ver solução completaQuestão 182
Considere a curva dada pela equação implícita
a- Calcule em termos de e .
b- Usando o resultado do item anterior, determine a equação da reta tangente à curva no ponto (3,1).
Ver solução completaQuestão 183
Calcule, usando as regras de derivação, as derivadas das seguintes funções (Não precisa simplificar as respostas finais, mas nas mesmas todas as derivadas envolvidas devem estar calculadas):
a.
Ver solução completaQuestão 185
C12) As outras funções hiperbólicas são definidas como abaixo.
Tangente hiperbólica. .
Cotangente hiperbólica. .
Secante hiperbólica. .
Cossecante hiperbólica. .
Calcule o que se pede.
b) A derivada de .
Ver solução completaQuestão 187
C12) As outras funções hiperbólicas são definidas como abaixo.
Tangente hiperbólica. .
Cotangente hiperbólica. .
Secante hiperbólica. .
Cossecante hiperbólica. .
Calcule o que se pede.
d) A derivada de .
Ver solução completaQuestão 190
Use a regra da cadeia para provar que (a) a derivada de uma função par é uma função ímpar e (b) a derivada de uma função ímpar é uma função par, desde que essas derivadas existam.
Ver solução completaQuestão 196
Muitas tabelas de derivadas não vêm com a regra da cadeia de forma explícita, ela aparece embutida nas fórmulas das derivadas elementares. Por exemplo, é muito comum você encontrar no lugar de . Neste exercício vamos aprender outro tipo de formulação.
Nesse exercício vamos aprender esse outro tipo de formulação.
d) Como você pode reobter a fórmula a partir de ?
e) Utilize um raciocínio análogo com e e descubra que
f) Usando a resposta do item anterior, calcule a derivada de .
Ver solução completaQuestão 197
Considere a função e suas derivadas definidas abaixo
Sobre o crescimento e decrescimento da função podemos afirmar que:
- é crescente nos intervalos e é decrescente nos intervalos
- é crescente nos intervalos e é decrescente nos intervalos
- é decrescente nos intervalos e é crescente nos intervalos
- é decrescente nos intervalos e é crescente nos intervalos
- é decrescente nos intervalos e é crescente nos intervalos
Questão 200
C11) As funções seno hiberbólico e cosseno hiperbólico são definidas como e , respectivamente.
b) Calcule a derivada de
Ver solução completaQuestão 201
C11) As funções seno hiberbólico e cosseno hiperbólico são definidas como e , respectivamente.
b) Calcule a derivada de
Ver solução completaQuestão 202
Seja , onde e é função derivável em . Sabendo que e podemos concluir que é igual a
Ver solução completaQuestão 203
C12) As outras funções hiperbólicas são definidas como abaixo.
Tangente hiperbólica. .
Cotangente hiperbólica. .
Secante hiperbólica. .
Cossecante hiperbólica. .
Calcule o que se pede.
c) A derivada de .
Ver solução completaQuestão 205
Seja , onde e é uma função derivável em . Sabendo que e podemos concluir que é igual a
.
.
.
.
.
Ver solução completaQuestão 206
Usando as regras de derivação, calcule a derivada das seguintes funções:
(a) .
(b) .
(c) .
Ver solução completaQuestão 207
C12) As outras funções hiperbólicas são definidas como abaixo.
Tangente hiperbólica. .
Cotangente hiperbólica. .
Secante hiperbólica. .
Cossecante hiperbólica. .
Calcule o que se pede.
a) A derivada de .
Ver solução completaQuestão 210
C6. Já vimos que a função |x| não é diferençável em x = 0, mas que a derivada existe em todos os outros pontos (igual a −1 se x é negativo e 1 se x é positivo). Nesse exercício vamos usar um artifício para trabalhar com a derivada de funções com m´ondulo sem ter que separar em partes.
a) Verifique que para todo .
b) Pelo item (a), a função h(x) = |x| é a composição das funções . Use isso e a regra da cadeia para encontrar . Verifique que sua resposta está de acordo com o esperado.
c)Utilize a formula descoberta no item anterior e a regra da cadeia para calculara a derivada de
Ver solução completaQuestão 213
Muitas vezes quando vamos modelar um problema físico, uma equação diferencial é obtida. Por exemplo, ao aplicar as leis da Física ao problema de um objeto em queda livre em que supõe-se que a resistência do ar é proporcional à velocidade, a equação diferencial obtida para a velocidade do objeto é , em que é a massa do objeto, é a aceleração da gravidade e k é a constante de proporcionalidade associada à resistência do ar. Mostre que é uma solução para a equação.
Ver solução completaQuestão 215
Considere a função
Então é igual a?
- 1/4
Não é necessário justificativa.
Ver solução completaQuestão 216
Muitas tabelas de derivadas não vêm com a regra da cadeia de forma explícita, ela aparece embutida nas fórmulas das derivadas elementares. Por exemplo, é muito comum você encontrar no lugar de . Neste exercício vamos aprender outro tipo de formulação.
Nesse exercício vamos aprender esse outro tipo de formulação.
g) Repita a ideia para as derivadas elementares que você conhece e construa sua nova tabela de derivadas já com a regra da cadeia embutida. Após concluir o resultado, perceba que todas elas são construídas da mesma forma: substitui-se na fórmula original por e multiplica-se a derivada por .
Ver solução completaQuestão 217
A regra da cadeia diz que
a) Aplique a fórmula acima duas vezes em sequência e encontre uma regra para a derivada da composição de três funções.
b) Estenda seu raciocínio para encontrar uma fórmula para a derivada da composição de funções.
c) Utilize a fórmula descoberta para calcular a derivada de .
Ver solução completaQuestão 220
23. Determine , e reais para que os gráficos das funções e sejam tangentes no ponto .
Ver solução completaQuestão 221
Considere uma função diferenciável e definida por .
Sabendo que , calcule
Ver solução completaQuestão 223
C11) As funções seno hiberbólico e cosseno hiperbólico são definidas como e , respectivamente.
c) Calcule a derivada de
Ver solução completa
Questão 226
O comprimento , a largura e a altura de uma caixa variam com o tempo . Em um determinado instante as dimensões são , e . Sabe-se que e estão aumentando a uma taxa de , enquanto está decrescendo a uma taxa de . Encontre a taxa de variação do volume da caixa no instante .
Ver solução completaQuestão 229
Nos exercícios , e , encontre , se é definida implicitamente pela equação dada.
Ver solução completaQuestão 232
As curvas
São percorridas no sentido anti-horário e considere um campo de classe no domínio tal que:
Qual o valor da integral de linha ?
Ver solução completaQuestão 235
Suponha que exista a função tal que para todo vale a seguinte relação:
Calcule , sendo Conclua que é constante sobre a elipse .
Ver solução completaQuestão 236
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Ver solução completaQuestão 249
10) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 250
14) Derive a função. (Se possível, simplifique a função e/ou a derivada da função).
Ver solução completaQuestão 253
Considere as funções e . Sabendo que e são funções deriváveis em seus domínios, a função composta tem derivada dada por:
Ver solução completa
Questão 254
Cristais de clorato de sódio são fáceis de crescer no formato de cubos permitindo uma solução de água e clorato de sódio evaporar vagarosamente. Se for o volume de cada cubo com comprimento de lado :
Mostre que a taxa de variação do volume de cada cubo em relação ao comprimento da aresta é igual a metade da área da superfície do cubo.
Ver solução completaQuestão 257
Um silo tem a forma de uma pirâmide de base quadrada invertida, com uma altura de m e diagonal da base de m. O tanque se esvazia de um líquido não viscoso à taxa de . Com que velocidade se encontra o nível de líquido quando a altura dele estiver a m do fim?
Ver solução completaQuestão 262
10. (1EE-2017.2-Adaptada) Calcule as derivadas das seguintes funções:
b)
Ver solução completaQuestão 265
Muitas tabelas de derivadas não vêm com a regra da cadeia de forma explícita, ela aparece embutida nas fórmulas das derivadas elementares. Por exemplo, é muito comum você encontrar no lugar de . Neste exercício vamos aprender outro tipo de formulação.
Nesse exercício vamos aprender esse outro tipo de formulação.
a) Sejam e (pense aqui que é uma função de que omitimos o parêntesis com x) e considere . Escreva quem é explicitamente.
b) Nas mesmas condições do exercício acima, determine , deixando a resposta em termos de .
(c) Juntando os itens (a) e (b) você descobriu que . Essa fórmula pode ser lida como “a derivada do seno de alguma coisa é a derivada da coisa vezes o cosseno da coisa”. Sem passar pela formulação da regra da cadeia original, utilize essa fórmula para determinar a derivada de
Ver solução completaQuestão 266
Questão 3. Considere um triângulo retângulo de catetos e e seja o ângulo adjacente a . Calcule e e aplique ao caso , .
Ver solução completaQuestão 267
1. Para os itens abaixo, use Regra da Cadeia e as técnicas de derivação.
b)
Ver solução completaQuestão 269
A quantidade de carga em coulombs (C) que passa através de uma seção reta de um fio até
o instante (medido em segundos) é dada por
Calcule a primeira derivada da função
Encontre a corrente quando: e
Ver solução completaQuestão 274
Um ponto se move na parábola conforme passa o tempo. Seja as coordenadas do ponto num tempo . Suponha que e são deriváveis e que . Em que ponto da parábola a velocidade da projeção do eixo é o triplo da velocidade da projeção do eixo ?
Ver solução completaQuestão 279
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
Encontre a velocidade desse movimento no instante .
Ver solução completaQuestão 280
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
Quando a velocidade é máxima?
Ver solução completaQuestão 283
1. Para os itens abaixo, use Regra da Cadeia e as técnicas de derivação.
a)
Ver solução completaQuestão 288
Uma equação em que a incógnita é uma função é chamada de . Quando há derivadas nessa equação, chamamos de . Assim como para equações tradicionais, uma função é uma solução da equação se, ao ser substituída no lugar da incógnita torna a igualdade verdadeira (igualdade do ponto de vista de funções, válida para todo valor de x). Mostre que é uma solução da equação .
Ver solução completaQuestão 289
Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo:
d)
Ver solução completaQuestão 290
Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo:
e)
Ver solução completaQuestão 296
Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo:
c)
Ver solução completaQuestão 302
3) Se é uma função derivável e positiva, então . Vamos usar este fato para calcular a derivada da função
Tomando o logarítmo nos dois lados, e lembrando que a função logaritmo transforma produtos em soma e potências em produtos, obtemos
Derivando, obtemos
e, portanto,
O procedimento acima é chamado de derivação logarítmica. Use-o para derivar as funções abaixo.
(b)
Ver solução completaQuestão 305
Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro para oeste a . A que taxa está crescendo a distância entre os carros duas horas depois?
Um carro A está se movimentando para o oeste a 90km/h e o carro B está se movimentando para o norte a 100 km/h. Ambos vão em direção à interseção de duas estradas. A que taxas os carros se aproximam um do outro quando o carro A está a 60 m e o carro B está a 80 m da interseção?
Ver solução completaQuestão 306
3) Se é uma função derivável e positiva, então . Vamos usar este fato para calcular a derivada da função
Tomando o logarítmo nos dois lados, e lembrando que a função logaritmo transforma produtos em soma e potências em produtos, obtemos
Derivando, obtemos
e, portanto,
O procedimento acima é chamado de derivação logarítmica. Use-o para derivar as funções abaixo.
(a)
Ver solução completaQuestão 307
A quantidade de carga , em coulombs (C), que passa através de um ponto em um fio até o instante (medido em segundos) é dada por
Em que e são constantes. Determina a corrente neste ponto do fio no instante t. Quais são as unidades de medida?
Ver solução completaQuestão 311
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função
Em que é medido em horas. No instante a população é de 20 células e está crescendo a uma taxa de . Encontre os valores de e . De acordo com este modelo, o que ocorre com a população de levedura depois de muito tempo?
Ver solução completaQuestão 315
Uma câmera filma o atleta em sua corrida até a linha de chegada. A distância entre o atleta e a chegada é , a distância entre a câmera e a linha de chegada vale e, para manter o foco no atleta, a câmera faz com a linha de chegada o ângulo , conforme a figura. No instante , o atleta cruza a linha de chegada e a velocidade angular da câmera é
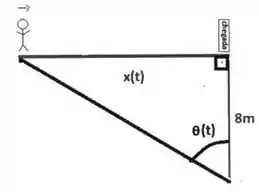
Argumente que
Com o auxílio da regra da cadeia, calcule a derivada
Determine a velocidade do atleta quando ele cruza a linha de chegada.
Ver solução completaQuestão 317
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
Faça o desenho dos gráficos da velocidade e posição,
Ver solução completaQuestão 318
O deslocamento de uma partícula sobre uma corda vibrante é dado pela equação
Encontre a velocidade da partícula após t segundos.
Ver solução completaQuestão 320
C3. Encontre os pontos do gráfico da função nos quais a reta tangente ao gráfico é paralela à reta .
Ver solução completaQuestão 324
Determine a diferencial das funções abaixo, com os valores de e indicados
Questão 326
Seja a equação do plano tangente ao gráfico de no ponto . Se , e , calcule .
Ver solução completaQuestão 332
Faça o que se pede em cada item, indicando claramente a(s) propriedade(s) utilizada(s) durantes os respectivos cálculos:
(a) Sendo , obtenha
Ver solução completaQuestão 333
9 - Suponha que a temperatura em um ponto de uma placa de metal seja . Uma formiga, andando sobre a placa, percorre um círculo de raio 5 centrado na origem. Qual é a maior e a menor temperaturas encontradas pela formiga?
Ver solução completaQuestão 357
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
Encontre a fórmula Fase-Amplitude desse movimento.
Ver solução completaQuestão 358
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
Quando a massa passa pela posição de equilíbrio pela primeira vez?
Ver solução completaQuestão 359
Uma faixa elástica é pendurada em um gancho e uma massa está presa na extremidade inferior
da faixa. Quando a massa é puxada para baixo e então solta, ela oscila verticalmente. A equação do movimento é
onde é medido em centímetros e , em segundos. (Consideramos o sentido positivo como sendo
para baixo.)
A que distância da posição de equilíbrio a massa chega?
Ver solução completaQuestão 366
Um caminhão descarrega areia a uma taxa de 3m³/min de tal forma que a areai descarregada tem um formato de cone em que a altura é igual ao diâmetro da base. Determine a taxa de crescimento da altura da pilha quando a altura for igual a 3m.
Ver solução completaQuestão 367
Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo:
f)
Ver solução completaQuestão 368
- Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo.
-
Ver solução completaQuestão 369
Supondo que e , use a regra da cadeia para calcular a derivada nos itens abaixo:
b)
Ver solução completaQuestão 371
Um ponto move-se ao longo de uma elipse . A abscissa está variando a uma velocidade . Mostre que
a)
b)
Ver solução completaQuestão 373
Derive as funções dos itens a) e b) e calcule o limite do item c)
a)
b)
c)
Ver solução completaQuestão 374
Calcule as derivadas sucessivas das funções
Em seguida, para cada uma delas determine uma lei de formação, ou seja, expresse
Ver solução completaQuestão 375
Indique por o trabalho realizado por um gás ideal ao se expandir isotermicamente desde um volume inicial até um volume V. podemos mostrar que em um unidades apropriadas, , onde é uma constante que depende da temperaturas e do número de mols do gás. Suponha que o volume seja uma função do tempo dada por . A potência gerada pelo sistema é a taxa de variação do trabalho em relação ao tempo.
- Encontre as derivadas e
- Encontre a expressão da potência do sistema,
- Sabendo que obtenha a potência do sistema quando o volume é 33.
Questão 376
Utilizando as regras de derivação, calcule a derivada das seguintes funçōes:e)
Ver solução completaQuestão 377
Utilizando as regras de derivação, calcule a derivada das seguintes funçōes:f)
Ver solução completaQuestão 378
Para cada uma das funções , em que e são dadas a seguir, faça o que se pede
(a) e
(a.a) Reescreva f (x), usando uma propriedade dos logaritmos, como
em que e . Em seguida, use a regra da cadeia para obter .
Ver solução completaQuestão 379
Para cada uma das funções , em que e são dadas a seguir, faça o que se pede
(b) e
(b.a) Reescreva f (x), usando uma propriedade dos logaritmos, como
em que e . Em seguida, use a regra da cadeia para obter .
Ver solução completaQuestão 380
Para cada uma das funções , em que e são dadas a seguir, faça o que se pede
(c) e
(c.a) Reescreva f (x), usando uma propriedade dos logaritmos, como
em que e . Em seguida, use a regra da cadeia para obter .
Ver solução completaQuestão 389
4.1. Suponha que seja uma função injetora, derivável, e que sua inversa, , também seja derivável. Mostre que
Ver solução completaQuestão 405
6. (b) Prove que a reta tangente ao gráfico de no ponto intercepta o gráfico apenas neste ponto
Ver solução completaQuestão 406
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Ver solução completaQuestão 408
3b) Considere a função dada por . Seja a função tal que seu valor em vale e sua derivada nesse mesmo valor vale . Calcule
Ver solução completaQuestão 414
7) Dizemos que é um ponto de inflexão de uma função se a concavidade de muda em .
A soma dos valores dos pontos de inflexão de é igual a:
Questão 415
Derive a função (se possível, simplifique antes e/ou depois de derivar).
Ver solução completa
Questão 418
Determine as derivadas das funções
em que é uma constante real e um natural maior do que .
Ver solução completaQuestão 428
Utilizando as regras de derivação, calcule a derivada das seguintes funçōes:
a)
Ver solução completaQuestão 429
Utilizando as regras de derivação, calcule a derivada das seguintes funções:
c)
Ver solução completaQuestão 430
Utilizando as regras de derivacão, calcule a derivada das seguintes funcōes:
d)
Ver solução completaQuestão 434
O deslocamento de uma partícula sobre uma corda vibrante é dado pela equação
Em quais instantes de tempo a partícula está parada?
Ver solução completaQuestão 447
O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:
em que s é medida em centímetros e t em segundos.
Encontre os instantes de tempo nos quais a partícula se encontra em repouso.
Ver solução completaQuestão 449
O movimento de uma mola sujeita a uma força de atrito é frequentemente modelado pelo produto de uma função exponencial e uma função seno. Suponha que a equação do movimento de um ponto sobre essa mole é:
em que s é medida em centímetros e t em segundos.
Encontre os instantes de tempo nos quais a partícula se encontra em repouso.
Ver solução completaQuestão 452
Seja uma função harmônica no aberto A, ou seja, , para todo . Sejam ainda funções de classe no aberto B tais que e satisfaçam e .
b. Mostre que
Ver solução completa