Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.2 - Ex. 44
Dado que é a função definida por
- Ache e mostre que
- Faça um esboço do gráfico de
Passo 1
Na letra a deste exercício precisamos descobrir o limite para a função dada quando está se aproximando de 2. Descoberto o valor do limite vamos compara com o valor da função no ponto .
Para começar vamos resolver o limite.
Passo 2
Para a letra a precisamos resolver:
Já que é diferente de 2.
Pelo Teorema 1:
Pelo enunciado observamos que:
Então:
Passo 3
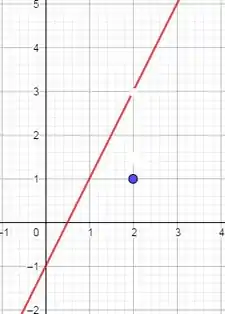
Para a letra b calculamos a função para os valores de diferentes de 2, e neste ponto a função assumirá o valor 1.
Desenhando o gráfico:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:d) lim x → - ∞ f x
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:a) lim x → 2 + f ( x )
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:d) lim x → - ∞ f ( x )
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:e) lim x → - ∞ f ( x )
Seja f ( x ) a função definida pelo gráfico:Intuitivamente, encontre se existir:b) lim x → 1 - f ( x )