Seja a função definida pelo gráfico:

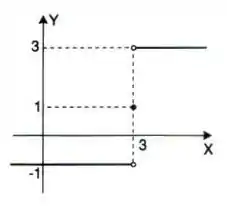
Intuitivamente, encontre se existir:

d)

Então pessoal, o que o enunciado quer é que observemos o gráfico e tentemos concluir se há algum valor para o qual a função tende quando se aproxima de , ou seja, quando é muito grande negativamente. Se observarmos o gráfico, antes de a função é totalmente constante com valor , sendo assim, podemos concluir o seguinte:

O resultado faz sentido porque apesar de não sabermos exatamente quanto vale o valor de quando , pelo gráfico notamos que aparenta ser , então é o que devemos acreditar! E essa aí é a nossa resposta!