Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.6 - Ex. 4d
Seja a função definida pelo gráfico:
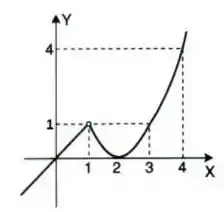
Intuitivamente, encontre se existir:
d)
Passo 1
Então pessoal, o que o enunciado quer é que observemos o gráfico e tentemos concluir se há algum valor para o qual a função tende quando é muito grande negativamente! Se observarmos o gráfico, poderemos notar que quanto mais diminui, mais também diminui, uma vez que se trata de uma função linear. Dessa forma, para um infinitamente grande negativamente o resultado também será um infinitamente grande negativamente, não é mesmo? Logo:
E esse é o nosso resultado!
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 23 a 42, prove que o limite é o número indicado, aplicando a Definição 2.1.1.37) lim x → 5 x ² - 3 x = 1 0 ²
Nos exercícios de 23 a 42, prove que o limite é o número indicado, aplicando a Definição 2.1.1.35) lim x → 2 x ² + 2 x - 1 = 7 ²
Nos exercícios de 23 a 42, prove que o limite é o número indicado, aplicando a Definição 2.1.1.36) lim x → - 3 x ² = 9 ²
Nos exercícios de 23 a 42, prove que o limite é o número indicado, aplicando a Definição 2.1.1.34) lim x → 3 x ² - 9 x - 3 = 6 ²
Prove que lim x → a x ² = a ² ² ², se a for qualquer número negativo.