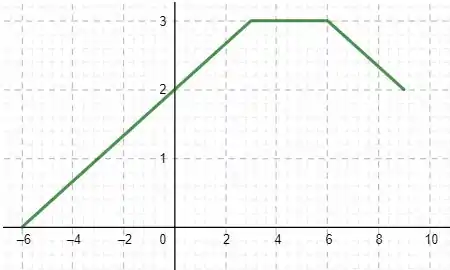
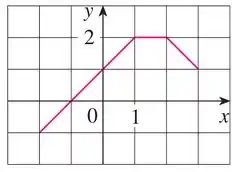
É dado do gráfico de f . Esboce os gráficos das seguintes funções:d) f 1 3 x + 1

Enunciado

Eaeee, belezinha?? Bom.. a questão nos dá o seguinte esboço de gráfico de uma função :

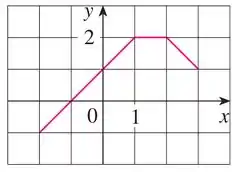
Com isso, a questão quer que esbocemos uma função que podemos chamar de que é dada da seguinte forma:

Mas como a gente faz isso??

Bom... para resolver isso a gente tem que comparar essas duas funções...

Ainda não entendeu?? Então bora junto porque não tem coisa melhor do que explicar com o próprio exemplo hehe 😉

Bom... perceba que a única diferença entre e é aquele multiplicando e aquela soma com . Se não fosse por isso as duas funções seriam iguais.

Então vamos por partes...

Sabe o que esse dentro de significa??

Significa que estamos esticando o gráfico horizontalmente, por um fator de unidades. Ele vai sofrer uma expansão lateral.

Por outro lado, se tivéssemos multiplicando por , estaríamos comprimindo o gráfico em unidades.

Já para o que está somando, significa que temos um deslocamento em unidade no sentido vertical.

Com essas informações, temos o seguinte gráfico:

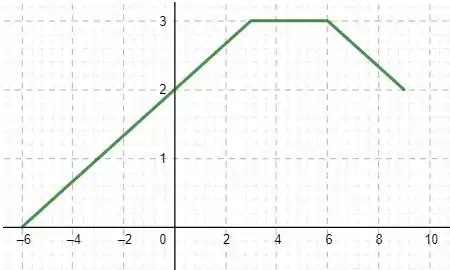
Entendeu direitinho?? Responde aee 😉