Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 3

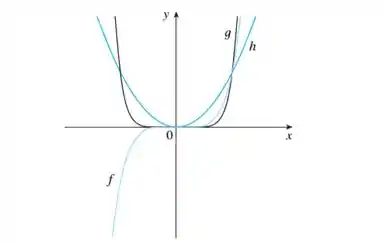
Associe cada equação a seu gráfico. Explique sua escolha. (Não use computador ou calculadora gráfica)

Passo 1

E aí galera, tudo bom?

Essa questão aqui é sobre gráficos de uma função potência (que é uma função polinomial com somente um termo).

Temos que saber que, quando temos um expoente par em uma função potência, seu formato é similar ao de uma parábola , mas um pouco mais achatada no meio e mais inclinada ao se afastar da origem.

Caso o expoente seja ímpar e maior que , teremos que os gráficos serão próximos do gráfico de , com o meio sendo mais achatado e as parte mais afastadas da origem sendo mais inclinadas.

Dá uma olhada no gráfico de :

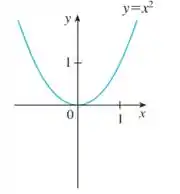
E de :

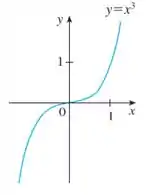
Sabendo disso, podemos identificar os gráficos.

Passo 2

a) A função é a que corresponde à , pois seu gráfico é uma parábola. Essa já tava entregue.

Tranquilo até aqui? 😐

Passo 3

b) Com relação à expressão , como seu expoente é ímpar, seu gráfico deve ser parecido com a de uma função cúbica . A única opção possível vai ser que o gráfico correspondente é o de , tranquilo?

Legal, né? 😊

Passo 4

Por último, temos o gráfico de . Por eliminação, já sabemos que seu gráfico é o de . E realmente é verdade: O gráfico de lembra muito uma parábola, não é mesmo? Só que mais achatada no meio e mais inclinada conforme vai se afastando da origem, que é o comportamento esperado.