Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 39
Deduza as Equações I para o caso .
OBS:
As equações I são as equações paramétricas do cicloide dadas por
Passo 1
Olá, meu amigooo. Então, pronto para mais uma resolução?
A gente precisa deduzir as equações I:
Para quando:
Bom, imagina lá nossa circunferência rodando na reta, fazendo a cicloide.
Imagina que ela já tenha andado uma de modo que temos que arrumar outra forma para parametrizar, diferente da que já está no livro.
A situação é a seguinte:
Para resolver este problema, precisaremos encontrar as coordenadas do ponto . O ponto P está posicionado no círculo com raio que é fixo, mas à medida que o círculo rola ao longo do eixo , o ponto também rola com o círculo, traçando assim a curva. As coordenadas do ponto serão equações paramétricas para a curva, e o parâmetro será o ângulo de rotação . A posição do ponto antes de o círculo começar a rolar ao longo do eixo é considerada como a origem.
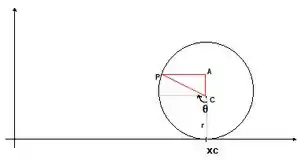
As coordenadas do nosso ponto são
E são elas que queremos descobrir, em função de e .
Passo 2
As coordenadas do nosso ponto serão:
Onde esse nada mais é do que a coordenada do centro da circunferência.
Vamos matar logo isso e descobrir essa coordenada.
Se você parar pra pensar, o centro da circunferência vai estar a uma distância da origem exatamente igual a distância que a nossa circunferência já andou. E que distância é essa?
É o arco .
E qual o comprimento de um arco de ângulo em uma circunferência de raio ?
Isso mesmo, . Portanto, a coordenada vale .
Tranquilo, né?
Já matamos uma parte então.
Passo 3
Agora, vamos ampliar esse triângulo aí de dentro da circunferência:
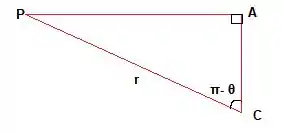
Está faltando descobrir o valor dos segmentos e .
Vamos usar relações fundamentais da trigonometria.
Isso aí é um triangulo retângulo, certo?
Então podemos dizer que
Daquelas relações que existem de cosseno e seno de a gente pode tirar que:
Daí temos que
E PRONTO!
Descobrimos quem faltava!
Passo 4
Agora substituindo tudo em
Temos
Que é exatamente aquilo que o enunciado dizia.
UFA, somo brabo, provamos tudo.
Resposta
Ver o desenvolvimento