Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 24
Associe os gráficos das equações paramétricas
Em com as curvas paramétricas rotuladas de . Justifique.
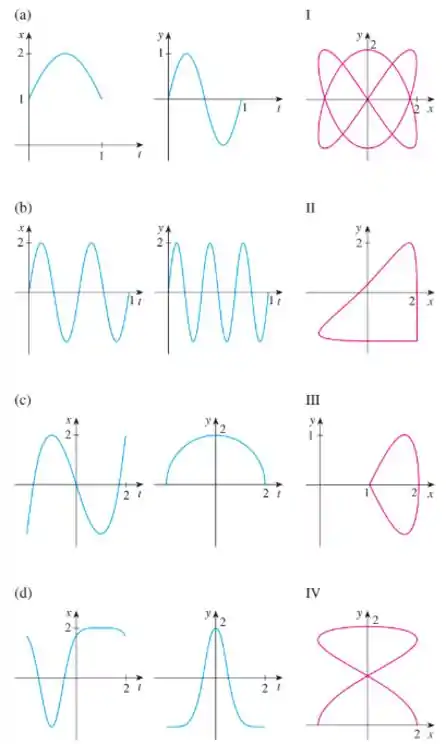
Passo 1
Bom, vamos começar os gráficos da letra .
Se você reparar, no primeiro gráfico, que é o gráfico de , vemos que varia de até .
E no segundo gráfico, que é o gráfico de , temos que
Dentre as opções das curvas parametrizadas, a única que tem
É a curva .
Pois é, parece uma questão super complexa e cabeluda, mas no fundo é só olhar a variação do e do .
Passo 2
Na letra B , vemos que tanto o quanto o variam de até . Além disso, o oscila quatro vezes o oscila seis vezes.
Todas essas coisas ocorrem também na curva da figura .
Passo 3
Na letra temos
E
Além disso, o está oscilando e oscila três vezes entre e . As mesmas coisas acontecem na curva parametrizada da figura .
Passo 4
Pra fechar, agora só sobrou a figura . Mas vamos explicar porque.
Na letra o varia de até e o também. Além disso, ambos oscilam entre esses valores duas vezes e o se mantem constante um tempinho em e o se mantem contante um tempinho em .
Acontece EXATAMENTE isso na curva .