Enunciado
Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 9
Demonstre que, se , aplicando o método de Newton para
que leva a se e a se . Desenhe uma figura que mostre o que ocorre.
Passo 1
Precisamos mostrar pra função dada que tem determinado valor a depender de , lembrando-se, é claro, que , ou seja, é um número positivo. Para isso utilizaremos o Método de Newton que nos diz o seguinte
Passo 2
Tomemos, inicialmente, e como teremos e vamos derivá-la obtendo o seguinte
Podemos, agora, substituir na equação Assim,
Passo 3
Agora, utilizaremos e como temos que teremos, então, e vamos derivá-la obtendo o seguinte
Podemos, agora, substituir na equação Assim,
Passo 4
A figura que ilustra o que ocorre é a seguinte
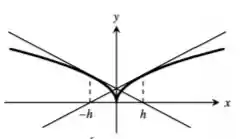
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios de 1 a 4, use o método de Newton para encontrar a raiz real da equação dada com quatro casas decimais. 6 x 3 + 9 x + 1 = 0
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. x 4 - 10 x + 5 = 0 ; a maior raiz positiva
Nos exercícios de 1 a 4, use o método de Newton para encontrar a raiz real da equação dada com quatro casas decimais. x 5 + x - 1 = 0
Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 6 3 , resolvendo a equação x 3 - 6 = 0
Nos exercícios de11 até 14, use o método de Newton para encontrar o radical dado com cinco casas decimais corretas. 7 3 , resolvendo a equação x 3 - 7 = 0