Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.6 - Ex. 29
Descreva como o gráfico de varia de acordo com a variação de c. Faça vários gráficos da família para ilustrar as tendências que você encontrou. Em particular, você deve investigar como os pontos de máximos e mínimos e os pontos de inflexão se movem quando c muda. Você também deve identificar valores de transição para c no qual a forma básica da curva muda.
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é descrever como a função muda então varia.
Tem ideia de como fazemos isso?
A questão ainda nos deu uma dica bacana... vamos verificar como os pontos extremos e os pontos de inflexão variam a medida que varia.
Para isso vamos calcular e e analisar como a variação de impacta nessas funções.
Bora começar!
Passo 2
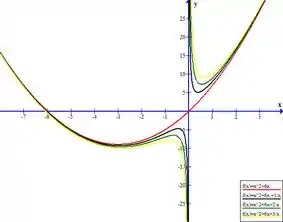
Vamos começar plotando o gráfico de para diferentes valores de ... vamos ver como se comporta quando , , 2 e .
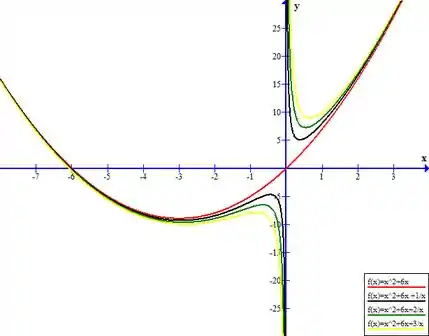
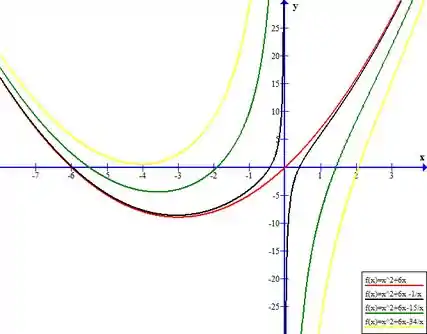
Mas e se for negativo?... vamos ver como se comporta em , e .
Quando O gráfico é uma parábola , que intercepta o eixo em e em . Sua concavidade é para cima e seu ponto de mínimo é .
Quando A parábola agora possui assíntotas quando , valendo pela esquerda e pela direita.
E quando Os pontos de interceptação são encontrados quando , variando conforme c aumenta. Por exemplo, para , as duas interceptações da função no lado negativo ficam entre e quando existe apenas uma interceptação. Isto é, esta parte do gráfico parece estar se deslocando para cima. Do lado positivo, a interceptação aumenta o valor de com a redução de .
Tranquilo até aqui?
Passo 3
Agora vamos analisar suas derivadas...
A primeira derivada de é dada pela regra da potência como:
Existe apenas uma raiz negativa quando .
Isto quer dizer que só vai existir um ponto de mínimo quando , com concavidade para cima, conforme mostra o gráfico. Para , não existe ponto de máximo ou mínimo.
Show?
Passo 4
A segunda derivada é dada pela regra da potência como:
Temos um ponto de inflexão quando , ou seja:
A partir destas derivadas e do gráfico, vemos que a concavidade quando é para cima apenas. Quando temos duas condições devido ao ponto de inflexão:
Concavidade para baixo no intervalo e para cima em Lembrando que c é negativo neste caso.
Para Existe apenas um ponto de interceptação quando , variando conforme c aumenta. Este ponto tende a se afastar para a esquerda conforme o crescimento de .
Quando , temos um ponto de mínimo, que aumenta de valor conforme aumenta. Isto faz com que o gráfico “ande para cima” de acordo com . De forma parecida ocorre quando , mas o gráfico anda para baixo e perde acentuação no ponto de máximo.
As concavidades então ficam: para cima quando e Para baixo quando
E aí! entendeu tudo? Responde Aí!
Resposta
