Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.1 - Ex. 28
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão da pra gente uma função definida por:
E pede pra gente esboçar o gráfico de à mão e usar esse esboço para encontrar os valores máximos e mínimos locais e absolutos de .
Então vamos fazer exatamente isso. Aqui precisamos lembrar que os pontos de máximo ou mínimo da função são os valores de que fazem com que a inclinação da reta tangente ao gráfico da função seja igual a zero.
Vamos esboçar o gráfico dessa função para ver isso acontecendo.
Passo 2
Para esboçar o gráfico de :
Para isso a gente vai olhar a função e calcular alguns pontos chaves, beleza?!
Vamos pegar , e que são os pontos extremos dos intervalos da nossa função!
Começando por , essa é uma parábola com concavidade pra baixo. Temos:
Esse que a gente terminou de calcular será uma bolinha aberta, pois o intervalo é , logo o zero não está incluso.
Agora , que é uma reta crescente. Temos:
Perfeito!
Passo 3
Agora é só desenhar!
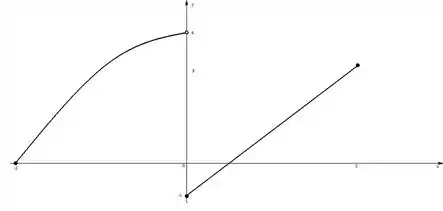
Passo 4
Pelo gráfico, podemos ver que temos
- Máximo absoluto: Nenhum- Como o que calculamos não pertence ao domínio, então não temos máximo absoluto.
- Máximo local: Nenhum – Pra ser um máximo local a gente precisa que seja menor na esquerda e na direita de detareminado ponto.
- Mínimo absoluto:
- Mínimo local: Nenhum- Pra ser um mínimo local a gente precisa que seja maior na esquerda e na direita de detareminado ponto.
Resposta
Mínimo absoluto: