Descrever as superfícies de nível da função.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade sobre superfícies de nível aqui.
Dada a função:
O que a gente precisa fazer e encontrar suas superfícies de nível.
Para descrever as superfícies de nível da função, basta fazer
As superfícies de nível são como as curvas de nível.
As curvas de nível estão em , enquanto as superfícies de nível em .
Então o que iremos encontrar é uma figura tridimensional, diferente das curvas de nível que são uma planificação.
Passo 2
Fazendo então:
Vamos utilizar um software gráfico para plotarmos essa figura para diferentes valores de . Iremos montar para
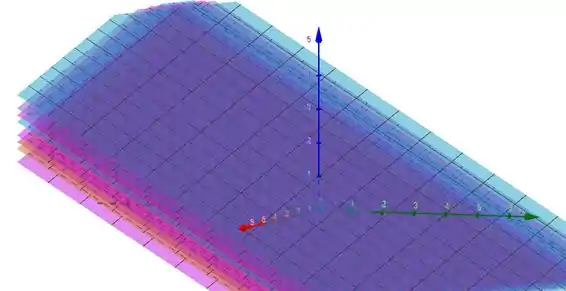
Trata-se de uma família de planos paralelos com vetor normal .
Resposta
Trata-se de uma família de planos paralelos com vetor normal .