Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 36
Dois mapas de contorno são mostrados. Uma é para uma função cujo gráfico é um cone. A outra é para uma função cujo gráfico é um parabolóide. Qual é qual e por quê?
Passo 1
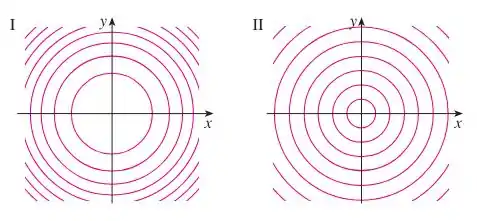
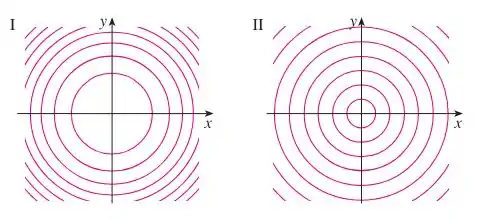
Eaee, belezinha?? Bom.. o enunciado nos deu as seguintes figuras que expressam curvas de níveis:
O enunciado nos disse que uma pertence a um cone e outra pertence a um parabolóide.
Queremos definir qual pertence a qual.
Para isso, temos que definir lembrar o que é um paraboloide e o que é um cone para podermos relacionar com as curvas de nível.
Passo 2
Bom... um cone entrado na origem é dado da seguinte forma:
Perceba que em um cone centrado na origem, o valor de cresce a uma taxa constante ao passo que andamos pelo eixo ou .
Agora, analisando um paraboloide simples centrado na origem, vemos que ele é dado da seguinte forma:
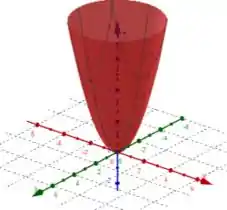
Perceba que em um paraboloide também centrado na origem, o valor de cresce mais suavemente perto da origem e mais rapidamente ao se afastar dela.
Passo 3
Olhando o espaçamento entre as curvas de nível (que indicam a taxa de crescimento do valor de ), percebe-se que no mapa II as curvas estão igualmente espaçadas, indicando uma taxa de crescimento constante para o valor de .
No mapa I, as curvas vão se aproximando ao se afastar da origem.
Logo, o mapa I representa a função do paraboloide.
O mapa II representa a função do cone.
Resposta
O mapa I representa a função do paraboloide.
O mapa II representa a função do cone.