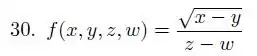Exercícios de Superfícies de Nível - Lista de Exercícios Resolvida

Descreva e esboce as superfícies de nível de .

Descreva as superfícies de nível da função abaixo.

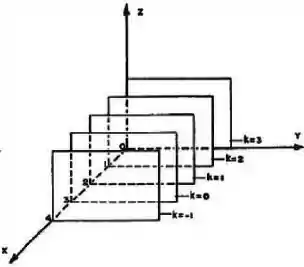
Na figura estão representadas superfícies de nível da função . Escreva uma expressão adequada para .

De acordo com a lei de gravitação universal de Newton, se uma partícula de massa está na origem de um sistema de coordenadas , então o módulo da força exercida sobre uma partícula de massa situada no ponto é dada por

Onde é a constante de gravitação universal. depende de quantas variáveis? Se e , descreva as superfícies de nível da função resultante.

Seja

Determine uma equação da superfície de nível que passa pelo ponto

a)

b)

c)

Resolva as questões abaixo:

1. Considere a função . Determine os conjuntos de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
2. Considere a função . Determine as curvas de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
3. Considere a função . Determine as superfícies de nível de .
4. Suponha que você chegue em uma sala de aula onde a única sentença escrita no quadro é “Faça um esboço do gráfico da função !”. Que desenho você faria?

Identifique as superfícies de nível da função , nos níveis e .

Identifique a superfície de nível da função que passa no ponto .

Descreva as superfícies de nível da função .

Descreva as superfícies de nível da função .

Seja definida por e , se . Mostre que

e

As superfícies de nível da função

Associadas aos níveis e podem se cortar? Justifique sua resposta!

De acordo com a lei de gravitação universal de Newton, se uma partícula de massa está na origem de um sistema de coordenadas , então o módulo da força exercida sobre uma partícula de massa situada no ponto é dada por

Onde é a constante de gravitação universal. depende de quantas variáveis? Se e , descreva as superfícies de nível da função resultante.

(Capítulo 14.1 – Exercício 66) Descreva as superfícies de nível da função.

Desenhar as curvas ou superfícies de nível dos seguintes campos escalares.

Esboce as superfícies de nível da função dada por para

Considere a região do espaço

1. Esboce hachurando
2. Esboce hachurando

2.1. Em cada caso, esboce a superfície de nível da função :

a. .

2.1. Em cada caso, esboce a superfície de nível da função :

c. .

2.1. Em cada caso, esboce a superfície de nível da função :

d. .

2.1. Em cada caso, esboce a superfície de nível da função :

e. .

2.1. Em cada caso, esboce a superfície de nível da função :

f. .

2.1. Em cada caso, esboce a superfície de nível da função :

g. .

2.1. Em cada caso, esboce a superfície de nível da função :

b. .