Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 15

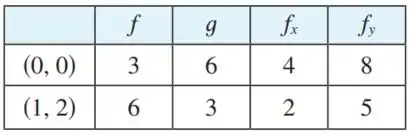
Suponha que f é uma função diferenciável de x e y , e g u , v = f ( e u + s e n v ,     e u + c o s   v ) . Use a tabela de valores para determinar g u ( 0,0 ) e g v ( 0,0 ) .

Passo 1

Show de bola, galera! Questãozinha de regra da cadeia, vamos lá!

A questão nos dá uma função g u , v = f ( x , y ) onde

x ( u ,   v ) = e u + s e n v

y ( u ,   v ) = e u + c o s   v

Basicamente

g u , v = f ( x u , v , y u , v )

E queremos encontrar g u ( 0,0 ) e g v ( 0,0 )

OK, mas como encontramos essas derivadas parciais numa função assim? Aí que entra a Regra da Cadeia Deluxe!

Para uma função g = f ( x , y ) onde x e y são funções de ( u ,   v ) , as derivadas parciais g u e g v são dadas por:

g u =     f x ⋅ ∂ x ∂ u +     f y ⋅ ∂ y ∂ u

g v =     f x ⋅ ∂ x ∂ v +     f y ⋅ ∂ y ∂ v

Dessa forma, vamos precisar calcular todos os termos dessas equações para encontrar as derivadas parciais g u e g v !

Passo 2

Vamos começar encontrando as derivadas parciais das “funções” x e y !

Para encontrar a derivada de x em u consideramos v constante:

∂ x ∂ u = d e u + s e n v d u

∂ x ∂ u = e u

Para encontrar a derivada de x em v consideramos u constante:

∂ x ∂ v = d e u + s e n v d v

∂ x ∂ v = ⁡ c o s ( v )

Para encontrar a derivada de y em u consideramos v constante:

∂ y ∂ u = d e u + c o s v d u

∂ y ∂ u = e u

Para encontrar a derivada de y em v consideramos u constante:

∂ y ∂ v = d e u + c o s v d v

∂ y ∂ v = ⁡ - s e n ( v )

Passo 3

Temos as derivadas parciais de x e y mas para completarmos as equações de g u e g v ainda precisamos de f x e   f y . Felizmente, a questão nos dá esses valores num gráfico!

Queremos g u ( 0,0 ) e g v ( 0,0 ) , então u ,   v = ( 0 ,   0 )

Para u ,   v = ( 0 ,   0 ) temos

x 0 ,   0 = e 0 + s e n 0

x 0 ,   0 = 1

y 0 ,   0 = e 0 + cos ⁡ 0

y 0 ,   0 = 2

Então vamos usar os valores de f x 1 ,   2 = 2 e f y 1 ,   2 = 5 para montar a equação!

Passo 4

Agora que temos todos os valores, podemos substituir tudo nas equações da regra da cadeia!

Para g u :

g u =     f x ⋅ ∂ x ∂ u +     f y ⋅ ∂ y ∂ u

g u =     2 ⋅ e u +     5 ⋅ e u

Substituindo o ponto

g u 0 ,   0 =     2 ⋅ e 0 +     5 ⋅ e 0

g u 0 ,   0 = 7

Para g v :

g v =     f x ⋅ ∂ x ∂ v +     f y ⋅ ∂ y ∂ v

g v =     2 ⋅ c o s v -     5 ⋅ s e n ( v )

Substituindo o ponto

g v 0 ,   0 =     2 ⋅ c o s 0 -     5 ⋅ s e n ( 0 )

g v 0 ,   0 = 2

Resposta

g u 0 ,   0 = 7

g v 0 ,   0 = 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar as derivadas parciais ∂ z ∂ ue∂ z ∂ v , usando a regra da cadeia z= x 2 + y 3,x = u 2 + 1,y =v 2 3
Verificar a regra da cadeia para a função z = f (e^x , - y^2) , f (u , v) = 2 u + v^2
Verificar a regra da cadeia para a função z = u^2 - v^2 , u = x + 1 , v = x y
Determinar as derivadas parciais ∂ z ∂ ue∂ z ∂ v , usando a regra da cadeia z= x e y,x = u v,y = u - v
Determinar as derivadas parciais ∂ z ∂ ue∂ z ∂ v , usando a regra da cadeia z= x 2 - y 2,x = u - 3 v,y = u + 2 v