Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1l
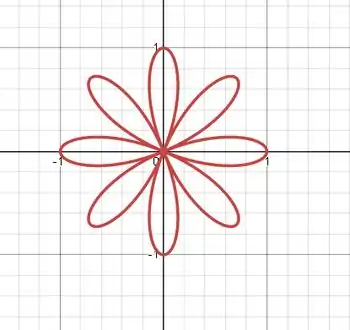
Desenhe a curva dada (coordenadas polares ).
Passo 1
Esse é um caso bem complicado e podemos se escolhermos todos os múltiplos dos Ângulos fundamentais, vamos ficar muito tempo e a tabela vai ficar gigante, por isso podemos escolher apenas múltiplos de e de .
Lembrando que esses valores tem que ser divididos por 4 pra podermos jogar na equação como se fosse uma equação de pra facilitar no desenho.
Passo 2
A tabela vai ficar:
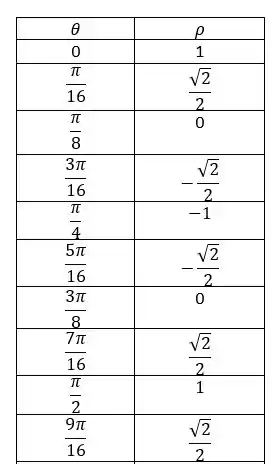
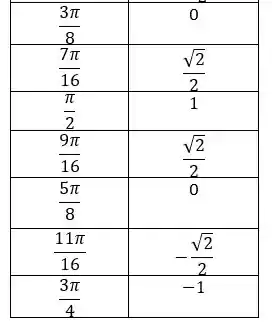
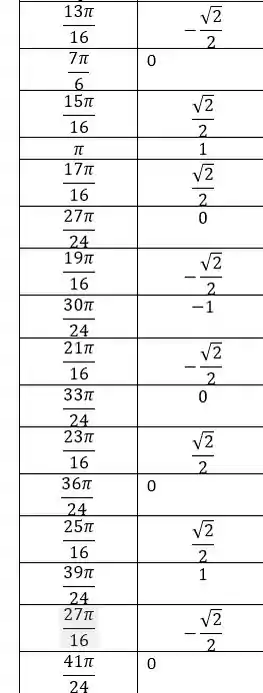
Passo 3
E o gráfico fica:
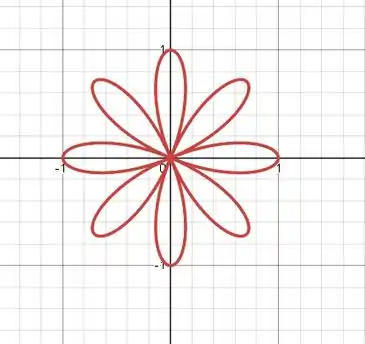
Resposta
Exercícios de Livros Relacionados
Determine a área da região” triangular” no primeiro quadrante, limitada acima pela curva y = e x 2 abaixo pela curva y = e - x 2 e à direita pelas curva y = 2 l n ( 2 )
Determine a área das regiões compreendidas entre y = s e n ( π x 2 ) e y = x
Determine a área da região” triangular” no primeiro quadrante, limitada acima pela curva y = e 2 x , abaixo pela curva y = e x e à direita pelas curva y = l n ( 3 ) .
Determine a área da região no primeiro quadrante, limitada à esquerda pelo eixo y , abaixo pela reta y = x 4 , acima à esquerda pela curva y = 1 + x e acima à direita pela curva y = 2 x .
Determine a área das regiões compreendidas entre y = c o s ( π x 2 ) e y = 1 - x 2