Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.1 - Ex. 4
Desenhe a imagem:
4.
Passo 1
O par de coordenadas (x,y) da nossa questão é , faremos o e
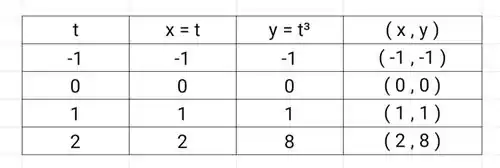Faremos uma tabela de alguns valores e então ligaremos os pontos e criaremos nossa imagem.
Portanto, será um polinômio de ordem 3 que passa pela origem.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Desenhe a imagem:5. F (t) = ( t^2 , t )
Desenhe a imagem:11. F (t) = (e^t c o s t , e^t s e n t) , t = 0
Desenhe a imagem. F t = 2 cos t ,2s e nt
Desenhe a imagem:12. F (t) = (s e n t , t)
1. Desenhe a imagem:a) F (t) = (1 , t , 1) , t in I R