Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.1 - Ex. 10
Desenhe a imagem.
Passo 1
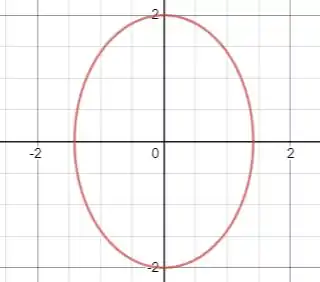
Essa é uma questão bem interessante em que temos que desenhar a imagem da curva
Note que podemos escrever e parametricamente como função de :
Isolando as funções trigonométricas:
Agora vem o pulo do gato: usando a relação fundamental trigonométrica
Passo 2
Essa curva é uma elipse centrada na origem com semieixo maior igual a na direção e semieixo menor na direção :
Resposta
Esboço de curva.
Exercícios de Livros Relacionados
Determine o domínio.F (t) = (t , sqrt((t - 2)/(t + 1)) , ln (5 - t^2) , e^(- t))
Seja F dada por F t = ln t , t , 1 - t 2 , t 2 .Determine o domínio de F .Calcule F 3 5 .
Sejam vec F (t) = (t , sen t , 2) e vec G (t) = (3 , t , t^2) . Calculevec F (t) * vec G ( t )
Calcule vec r (t) xx vec x ( t ) , onde vec r (t) = t vec i + 2 vec j + t^2 vec k e vec x (t) = t vec i - vec j + vec k .
Calcule u → t ⋅ v → ( t ) , onde u → t = sen ti → + cos tj → + tk → e v → t = sen ti → + cos t j → + k → .