Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.1 - Ex. 15
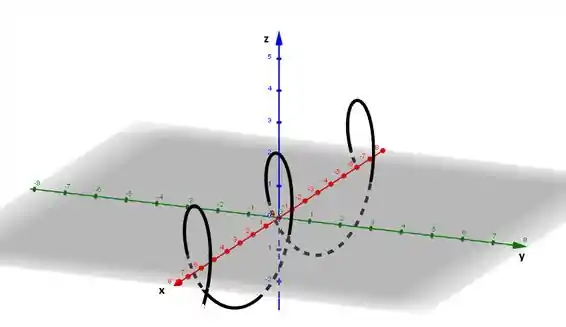
Desenhe as projeções da curva nos três planos coordenados. Use essas projeções para ajudá-lo a esboçar a curva.
Passo 1
Olá, meu amigo. A gente tem em mãos a equação:
E deveremos utilizar dela para desenharmos as projeções nos três planos coordenados.
Para desenharmos as projeções das curvas em cada plano coordenado precisamos primeiramente zerar uma das coordenadas, e analisar como fica cada plano.
Os gráficos, a gente criará utilizando o GeoGebra, pois confie em mim, será melhor do que você me ver desenhando na mão. Mas caso queira plotar o gráfico na não, construa uma tabela com valores distintos de , e obtenha pontos para e em função desse . Depois disso é só plotar no plano cartesiano.
Passo 2
Desta forma, no plano precisamos zerar a coordenada , ficando com:
Tendo então a função variando ao longo do eixo .
O plano , zeramos a coordenada :
Onde podemos fazer a seguinte manipulação:
Obtendo a elipse .
Por último no plano , zeramos a coordenada :
Tendo então a função variando ao longo do eixo .
Passo 3
Plotando o gráfico das projeções:
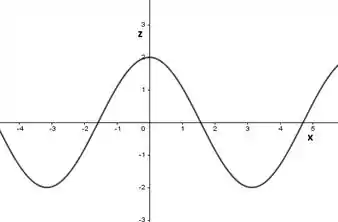
Plano :
Plano :
Plano :
Passo 4
Plotando o gráfico utilizando as projeções:
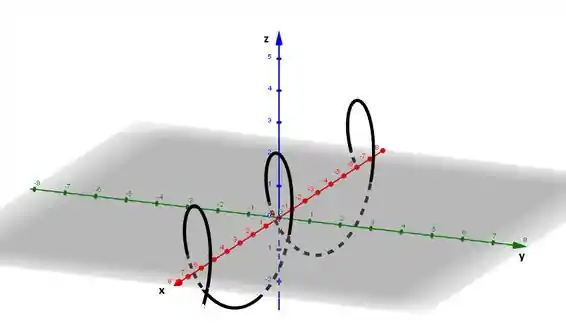
Resposta
