Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 31
Encontre as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.
Passo 1
Olá, meu amigo. Vou te auxiliar nessa resolução hoje.
Dada a curva parametrizada:
Queremos saber a equação paramétrica da reta tangente a essa curva, no ponto:
Em uma equação paramétrica do tipo:
A reta tangente dessa equação paramétrica é:
Onde:
É o ponto de tangencia, e:
É a derivada do nosso vetor no ponto que nos leva ao ponto de tangencia:
Passo 2
A equação vetorial da curva é
No ponto o valor do parâmetro é , como pode ser deduzido da segunda equação paraméteica da curva:
A derivada da função vetorial é encontrada abaixo, precisamos utilizar a regra do produto aqui, pois temos o produto de funções em e em :
Aplicando então a regra da cadeia e derivando:
Portanto, o vetor tangente no ponto especificado, ou seja, para , é
Passo 3
A reta tangente, cujas equações paramétricas procuramos, passa pelo ponto e é paralela ao vetor tangente:
Relembrando a equação geral:
Já temos tudo o que precisamos, então nossa equação fica:
Agora em formato paramétrico:
Com base nas equações paramétricas da curva e da reta é possível traçar os gráficos de ambas numa mesma tela utilizando softwares como mostrado abaixo:
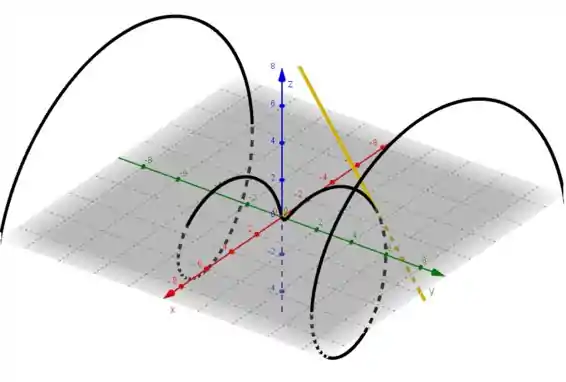
Nossa reta tangente é a amarela, e a nossa reta paramétrica é a preta.