Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.3 - Ex. 4
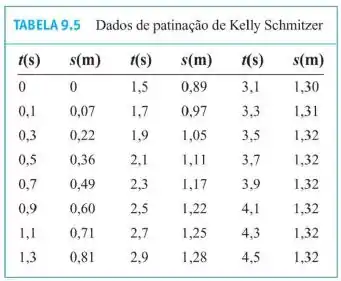
Deslizando até parar A Tabela 9.5 mostra a distância s ( em metros) em termos do instante t (em segundos) que Kelly Schmitzer percorreu de patins. Determine mn modelo para a sua posição na forma da Equação 2. Sua velocidade inicial era v0 = 0,80 m/s, sua massa, m = 49,90 kg (110 lb) e a distância total deslizada, 1,32 m.
Passo 1
Pela equação 2 temos que a distância total percorrida é dada por:
Passo 2
Analisando os dados no problema temos que:
m= 4,90 kg
m/s
k=?
S(t)=1,32 m (Distância total percorrida)
Passo 3
Com essas informações podemos obter o k, a fim de fazer o modelo completo. Assim, primeiro iremos obter a expressão da distância total, dada por:
Substituindo os valores temos:
Passo 4
Assim o modelo será dado por:
Resposta
Modelo será dado por:
Exercícios de Livros Relacionados
Nos problemas 29-34, encontre as trajetórias ortogonais das curvas dadas. r = 2 c 1 . cos θ
Nos problemas 29-34, encontre as trajetórias ortogonais das curvas dadas. r = c 1 1 + c o s ( θ )
Nos problemas 29-34, encontre as trajetórias ortogonais das curvas dadas. r 2 = c 1 . s e n 2 θ
Nos problemas 36-38, use os resultados do problema 35 para encontrar a família isogonal que intercepta a família a um parâmetro y = c 1 . x com o ângulo dado. α = 3 0 °
Mostre que duas curvas polares r = f 1 ( θ ) e r = f 2 ( θ ) são ortogonais em um ponto de interseção se, e somente se, t gψ 1 C 1 . t gψ 2 C 2 = - 1