Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 21

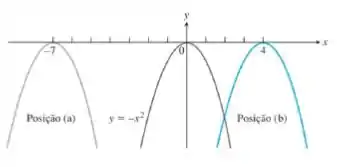
A figura a seguir mostra o gráfico de transladado para duas novas posições. Escreva equações para os novos gráficos.

Passo 1

Esta é uma questão simples. Como ela já nos deu a equação de uma das funções, basta analisarmos o que aconteceu com ela para conseguir identificar o gráfico das outras curvas. Isto é, ocorreu alguma translação? Se sim, foi vertical ou horizontal? Ou o que ocorreu foi uma rotação? Quantos graus foi a translação?

Vamos então começar por identificar o que ocorreu. Tanto para a posição quanto a , o que ocorreu foi uma translação horizontal. Uma translação horizontal é realizada da seguinte forma:

Em que é o número de unidades a ser transladada. Se , a função é transladada para a esquerda. Se negativo, para a direita. Vamos então identificar a equação de casa posição.

Passo 2

Começando pela posição , observamos que a curva foi transladada para a esquerda em 7 unidades. Portanto, . Logo, a nossa função é:

Passo 3

Já na posição , observamos que a curva foi transladada para a direita em 4 unidades. Portanto, . Logo, a nossa função é:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y =2 x - 2

Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = x - 2 - 1

Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = y = x 2 + 6 x + 4

Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = 1 - 2x + 3

Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção 1.2 e então aplicando as transformações apropriadas. y = x - 2