Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.10 - Ex. 31
31. Determinar algebricamente os valores de , tais que o gráfico de esteja abaixo do gráfico de , sendo e . Usando a ferramenta gráfica, traçar o gráfico das funções dadas e comparar os resultados.
Passo 1
Vamos aplicar os nossos conhecimentos de inequação e desenhar os gráficos de !
Só que antes vamos entender o que é o gráfico de estar abaixo de .
Ora, isso nos quer dizer que .
Passo 2
Na inequação, teremos que resolver isso:
Agora desenharemos o gráfico das funções do segundo grau! Para isso, precisaremos antes lembrar que uma função do grau tem como gráfico, uma parábola!
Para :
Faremos o primeiro ponto, em que substituiremos por .
O segundo ponto, substituiremos :
ou
E com concavidade para cima, pois !
Passo 3
Agora faremos o gráfico de :
Faremos o primeiro ponto, em que substituiremos por .
O segundo ponto, substituiremos :
ou
E com concavidade para baixo, já que :
Desenhando os dois gráficos num mesmo sistema de coordenadas, temos:
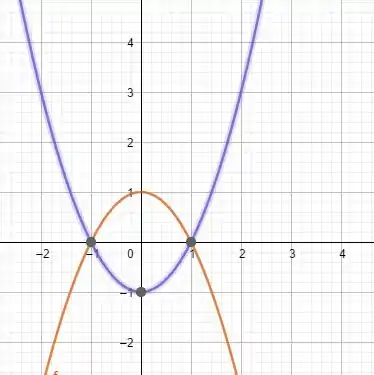
Em roxo, temos o gráfico de e em dourado temos o gráfico de
é maior que para pontos entre e , conforme achamos na equação!!!
O dourado fica acima do roxo, melhor dizendo!