Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 64
Determine as áreas das regiões compreendidas entre as retas e as curvas
E
Passo 1
Para podermos determinar a área de uma região compreendida entre duas curvas, precisamos obter um esboço do gráfico. Com ele, poderemos determinar qual o nosso intervalo de integração, qual curva está acima da outra e se há uma mudança neste comportamento. Sendo assim, vamos utilizar recursos gráficos para ajudar nesta visualização. Descoberto o intervalo e que ao longo deste intervalo, então a área entre as curvas e é dada por:
Desta forma, temos que identificar em cada caso quem é , e o intervalo .
Passo 2
Vamos começar por obter o esboço das curvas.
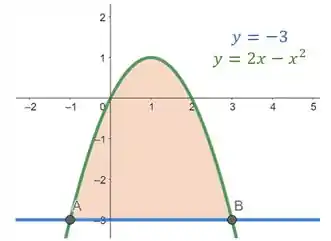
A nossa região está limitada acima pela função , abaixo por e o intervalo de integração é em que e são as coordenadas dos pontos A e B, pontos de interseção de e . Para calcular estas coordenadas basta igualar as duas funções e resolver a equação. Desta forma, temos:
Portanto, temos e . Logo, temos que e . Portanto, a nossa integral é:
Passo 3
Vamos resolver agora nossa integral.