Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes.
Passo 1
Para calcular essa integral vamos usar a Definição de uma Integral Imprópria do Tipo 1:
Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.
Passo 2
Primeiro vamos analisar qual regra usar para calcular essa integral, então mãos a massa: a expressão já tá simplificada, vamos então tentar fazer uma Integração por Partes:
Vamos fazer então e :
e
Vamos calcular para poder substituir na fórmula de Integração por partes:
Vamos usar uma substituição:
Vamos substituir agora:
Pronto, agora temos uma integral simples de resolver, vamos lá.
Passo 3
É fácil achar as primitivas da função, usando duas expressões da Tabela de Integrais Indefinidas:
Assim vamos ficar com:
Não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo:
Vamos substituir agora:
Pronto, agora temos uma integral simples de resolver, vamos lá.
Passo 4
Agora vamos usar uma substituição trigonométrica:
Vamos substituir agora:
Vamos manipular um pouco essa expressão usando a identidade trigonométrica e que :
Pronto, agora temos uma integral simples de resolver, vamos lá.
Passo 5
É fácil achar as primitivas da função, usando três expressões da Tabela de Integrais Indefinidas:
Assim vamos ficar com:
Calma, não terminou ainda, não esqueça de voltar para a variável , para isso vamos fazer um esquema pela figura abaixo:
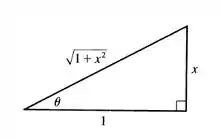
Temos então que:
Vamos substituir agora:
Vamos agora voltar a expressão original e problema resolvido:
Passo 6
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá:
A integral converge, pois o limite existe.
Resposta
Converge e tem valor