Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 26
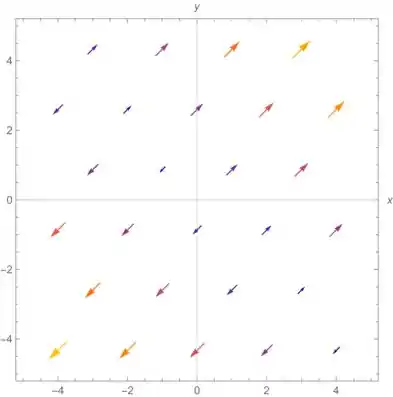
Determine o campo do vetor gradiente de e o desenhe.
Passo 1
Faala, galera!
Essa questão pede pra gente calcular e desenhar um campo vetorial gradiente de uma função
Como o gradiente é dado por:
Nosso primeiro objetivo vai ser encontrar quem são essas derivadas parciais, pra definir o campo vetorial.
Daí, vamos estudar como esse campo se comporta conforme mudamos o ponto . Vamos usar o módulo dele pra ver também como seu tamanho muda:
Por fim, com todas essas informações, podemos desenhar o campo!
Passo 2
Começamos derivando em função de , com constante:
Agora derivando em função de , considerando como constante:
Bom, o gradiente fica assim:
Passo 3
Com isso, já percebemos de cara que as duas coordenadas dos vetores do campo são iguais!
Ou seja, todos os vetores são paralelos a .
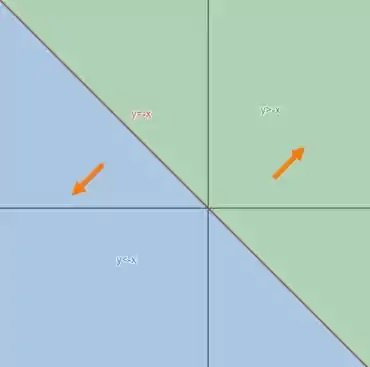
Além disso, o que define o sentido que eles apontam é o sinal de :
- Se , o vetor aponta pra cima e pra direita (sentidos positivos de e )
- Se , o vetor aponta pra baixo e pra esquerda (sentidos negativos de e )
- Se , o campo da , o que indica que não existe vetor.
Resumindo:
Passo 4
Por último, vamos ver os tamanhos dos vetores:
Então,
Ou seja, quanto maior o valor de , maior vai ser o tamanho do vetor. Isso quer dizer que vetores mais afastados de serão maiores que vetores mais próximos.
Com isso, conseguimos desenhar:
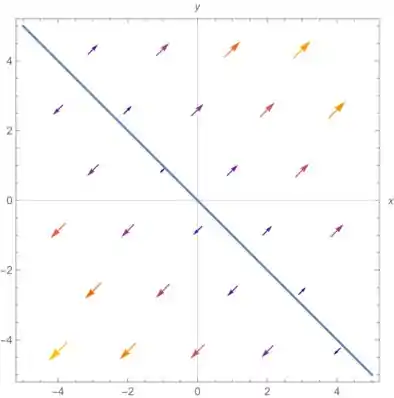
Essa reta em azul representa .
Resposta
