Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 31

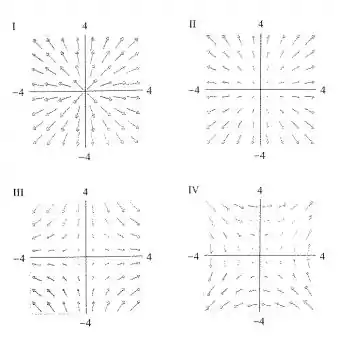
Case as funções com os desenhos de seus campos de vetor gradiente (rotulados de I-IV). Dê razões para suas escolhas.

f x , y = x 2 + y 2

Passo 1

Para podermos comparar o campo do vetor gradiente da nossa função com os desenhos (I-IV) do livro, precisamos primeiro determinar quem é este vetor gradiente. Ele é nada mais e nada menos do que um vetor de derivadas parciais. Isto é:

∇ f x , y = ∂ f ∂ x i + ∂ f ∂ y j

Portanto, precisamos obter as derivadas parciais da nossa função f . Desta forma,

∂ f ∂ x = 2 x

∂ f ∂ y = 2 y

Portanto, o gradiente da nossa função é:

∇ f x , y = y i + x j

Passo 2

Para podermos identificar qual desenho representa o campo vetorial do nosso gradiente, temos duas opções: utilizar um software para plotar e comparar (o jeito fácil), ou tentar fazer considerações no gradiente para identificar o desenho (o jeito difícil).

Como a questão nos pede para dar razões para identificar o desenho, vamos ter de trabalhar com o jeito difícil....

Bom, quando estamos no primeiro quadrante, temos x , y ≥ 0 . Com isto, o nosso vetor gradiente vai ter f x ≥ 0 e f y ≥ 0 (vetor aponta para a direita e para cima).

No quarto quadrante temos x ≥ 0 e y ≤ 0 . Por causa disto, temos f x ≥ 0 e f y ≤ 0 . Logo, o vetor aponta para direita e para baixo. Se continuarmos essa análise para os outros dois quadrantes, vamos confirmar que só existe uma figura que se enquadra com este caso.

Este desenho é o I.

Resposta

O desenho I representa o ∇ f .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O campo de velocidade de um fluido em movimento é dado por v → = ( 2 x , 2 y , - z ) . Calcular a circulação do fluido ao redor da curva fechada C , sendo C dada por r → t = cos ⁡ ti ^ + s e ntj ^ + 2
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:(c) triângulo de vértices ( 1,1 ) , ( - 1,1 ) e ( 0 , - 1 )
O campo de velocidade de um fluido em movimento é dado por v → = 3 j ^ + k ^ . Determinar a circulação ao fluido ao redor do quadrado de vértices A 0,0 , 0 ,B 2,0 , 0 , C 2,0 , 2 e D ( 0,0 , 2 ) .
Resolver o Exercício 27 para f → = ( 3 x z , 4 y z , 2 x y )
O campo de velocidade de um fluido em movimento é dado por v → = y , - x . Determinar a circulação do fluido ao redor do triângulo de vértices A ( 0,0 ) , B ( 2,0 ) e C ( 2,2 ) . Qual o sentido em que