Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 10
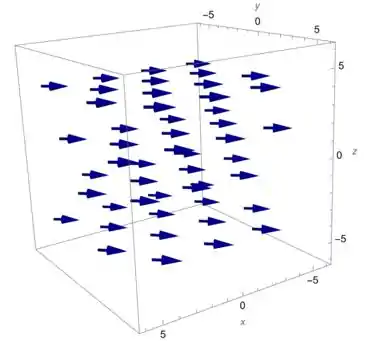
Esboce o campo vetorial , desenhando um diagrama como o da Figura 5 ou da Figura 9
Passo 1
Falaa, turma! Tudo bem?
Nessa questão, nossa missão é desenhar um campo vetorial
Com um desenho como dessas figuras:
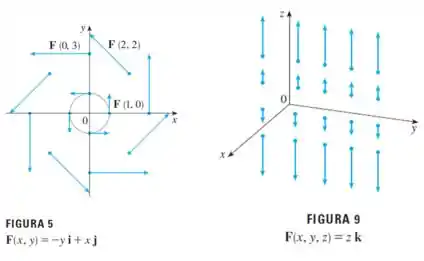
Como estamos no , nossa figura vai ficar como a .
O que precisamos fazer é ver como que essa expressão se comporta conforme mudamos o ponto .
Então, vamos desenhar os vetores de alguns pontos, pra representar o campo!
Passo 2
Bom, esse e são os versores que representam a segunda e primeira coordenadas de , respectivamente, o que significa que o campo pode ser escrito assim:
Ou seja, independente do ponto , nosso campo representa sempre o mesmo vetor .
Percebe que como , podemos desenhar esse vetor no :
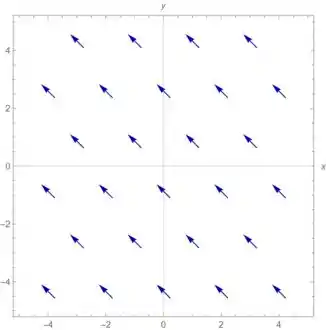
Então, no , esse campo fica assim:
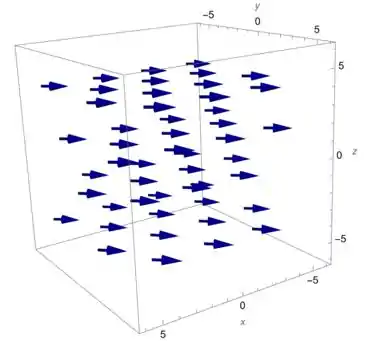
Resposta
Exercícios de Livros Relacionados
Verificar se as seguintes funções são harmônicas em algum domínio.g) f x , y = e x cos y
Verificar se as seguintes funções são harmônicas em algum domínio.d) f x , y , z = x 2 + y 2 + z 2
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:Circunferência de centro na origem e raio 2;
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:(b) elipse x 2 + 36 y 2 = 36
O campo de velocidade de um fluido em movimento é dado por v → = ( x , - y ) . Calcular a circulação do fluido ao redor da curva fechada C = C 1 ∪ C 2 ∪ C 3 , onde C 1 : Segmento de reta de A 0,0 e B