Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 70b
Determine o domínio da função .
Passo 1
E aí, pessoas! Bora pra mais uma?
Aqui temos que lembrar que o domínio de uma função é simplesmente os valores que o pode assumir para aquela função específica. Beleza?
Passo 2
Vamos olhar pra função: .
O que tá dentro pode ser qualquer positivo? Pode, pois existe de número positivo.
Pode ser qualquer negativo? Não, pois não existe de número negativo.
Pode ser 0? Não, pois não existe de 0.
Então, . Olha só o gráfico dessa parábola:
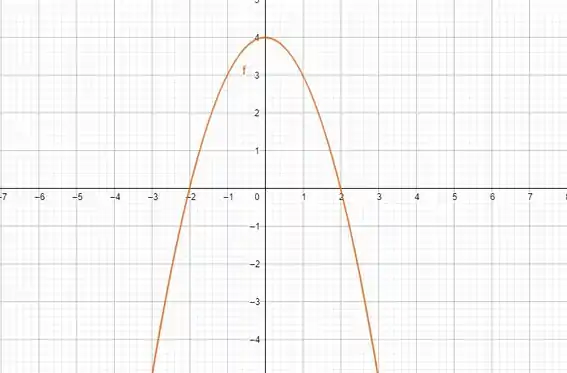
A gente tem que ver onde , que é no intervalo [-2,2].
Então:
Resposta
Exercícios de Livros Relacionados
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta19. Uma curva que cruza o eixo x em dois pontos distintos não pode ser o gráfico de uma função.
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta21. A imagem da função valor absoluto é o conjunto de todos os números reais positivos