Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 56

Uma tigela tem um formato que pode ser obtido pela revolução em torno do eixo y , do gráfico de y = x 2 2 entre y = 0 e y = 5

  1. Determine o volume da tigela.
  2. Taxas relacionadas. Se enchermos a tigela com água a taxa constante de 3unidades cúbicas por segundo, a que taxa o nível da água na tigela aumentará quando a água estiver com 4 unidades de profundidade?

Passo 1

Perceba que a região que desejamos calcular o volume é da forma:

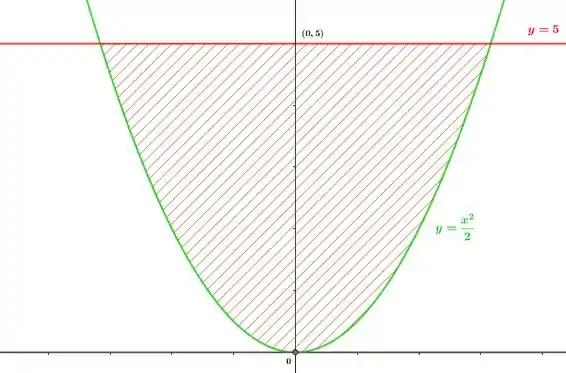
E de fato, quando rotacionarmos a região em torno do eixo y , teremos algo parecido com uma tigela, sendo assim para calcular o volume faremos

V = ∫ 0 5 π f y 2 d y

Mas para calcularmos em relação a y , precisamos manipular a expressão y = x 2 2 . Sendo assim teremos

y = x 2 2 ⇒ x = 2 y

Dessa maneira,

V = ∫ 0 5 π f y 2 d y = ∫ 0 5 π 2 y 2 d y = ∫ 0 5 π 2 y   d y

=   2 π ∫ 0 5 y   d y = 2 π     y 2 2 ​ 0 5 = π 5 2 - 0 2 = 25   π

Passo 2

Desejamos determinar a variação do volume em relação ao tempo , ou seja, d V d h isso significa que teremos que derivar o volume encontrado no item anterior, só que agora em relação à h ,   porém temos que lembrar que h depende de t . Dessa maneira derivaremos implicitamente, ou seja,

Lembrando que a = 5 temos

V t = 2 π     h 2 2 = 2 π 2 h .   h ' ( t ) 2 = 2 π h .   h ' ( t )

Utilizamos a expressão pois nesse casos y corresponde a altura, e neste caso varia com o passar do tempo

V ' ( t ) 2 π 2 h .   h ' ( t ) 2 = 2 π h .   h ' ( t )

Evidenciando h ' ( t ) teremos

h ' t = V ' t 2 π h

Como sabemos que V ' t = 3 e h = 4

h ' t = 3 2 π 4 = 3 8 π u n d 3 / s

Resposta

Item a. 25   π

Item b.   h ' t = 3 8 π u n d 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15. Volume de um orifício de uma esfera sólida Um orifício redondo de raio 3 pés é furado através do centro de uma esfera sólida de raio 2 pés. Determine o volume de material removido da esfera.
13. Determine o volume do sólido gerado pela rotação da região limitada pela curva x = e y 2 e pelas retas y = 0 , x = 0 e y = 1 em torno do eixo x .
A região entre a curva y = 1 / x 2 e o eixo x de x = 1 / 2 a x = 2 é girada em torno do eixo y , gerando um sólido. Determine o volume do sólido.
No Exercício 6 da Seção 6.2, giramos em torno do eixo y a região entre a curva y = 9 x / x 3 + 9 e o eixo x de x = 0 a x = 3 para gerar um sólido de volume 36 π . Em vez disso, se girarmos a região em
Determine o volume do sólido obtido com a rotação de cada região em torno do eixo y . A região é a região, no primeiro quadrante, limitada à esquerda pelo círculo x 2 + y 2 = 3 , à direita pela reta x