Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 9
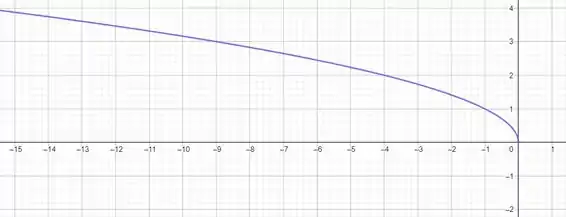
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos devagar que fica tranquilinho: primeiro o domínio, depois a imagem e por último vamos usar o que encontramos para esboçar o gráfico.
Passo 2
A nossa função é uma função raiz quadrada, então precisamos que o que está dentro da riz seja não-negtivo, ou seja:
Multiplicando os dois lados por e invertendo o sinal da desigualdade:
Daí temos o nosso domínio:
Passo 3
A nossa imagem será a imagem de qualquer função raiz com o domínio infinito: Podemos ver isso tirando a raiz quadrada dos dois lados da inequação que tínhamos na 1ª linha de cálculo do 2º passo.
Ou seja:
Passo 4
E o gráfico é tranquilo de fazer também, é só pegar o gráfico de e espelhá-lo no eixo e teremos o gráfico de :
Esse é o gráfico de :
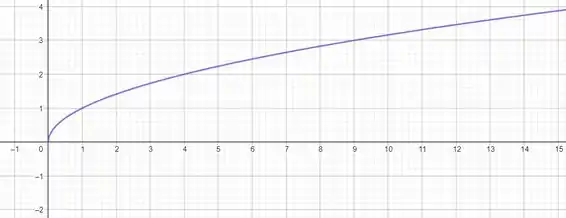
Fazendo a reflexão no eixo , temos a gráfico de
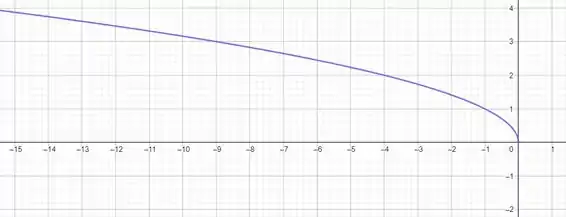
Resposta
Domínio:
Imagem:
