Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 3
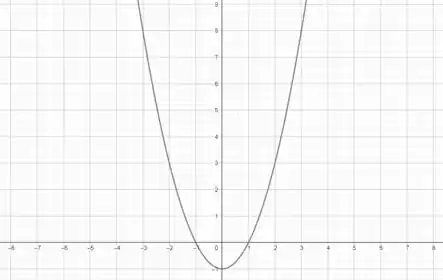
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Fala galera, tudo certo? Ó só, nossa função é essa:
Pô, mas não é que ela parece muito com:
Se parece um pato e faz quack como um pato, é um pato! Nossa nada mais é do que um polinômio de grau 2 onde:
E só isso já nos diz muito dessa função: sabemos que o gráfico dela é uma parábola e que seu domínio é todo o conjunto dos reais! Mas e sua imagem, qual será? Bem, sabemos que qualquer número ao quadrado é maior ou igual a :
Para qualquer valor de , vamos subtrair em ambos os lados da equação agora:
Ou seja:
Em outras palavras, aceita qualquer real, mas retorna sempre um número maior ou igual a . Seu domínio e imagem serão:
Passo 2
Bora pro esboço agora. Para fazer um esboço singelo de uma parábola, precisamos de dois parâmetros: o sinal do termo quadrático (se é positivo ou negativo) e o valor mínimo da imagem. Como vimos no passo anterior, nossa função é tal que:
Sabendo que o sinal de “” dita a orientação da concavidade da parábola de forma que:
- Se , a parábola terá concavidade para cima.
- Se , a parábola terá concavidade para baixo.
Basta pro nosso esboço a gente desenhar uma parábola com concavidade pra cima (já que ) em que a “ponta do copinho” toque o eixo em :
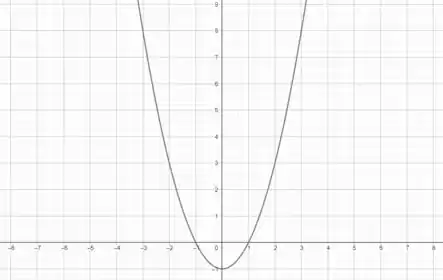
Resposta
