Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Não vai ter stress nenhum. Já tamo craque em função módulo! Vamos começar definindo o domínio, depois a imagem (com um cuidadinho extra) e pra fechar a questão a gente plota o gráfico.
Passo 2
Não temos restrição alguma no domínio. Nenhuma raiz quadrada, nenhuma função racional. Só temos o módulo e ele não faz nada com o domínio da nossa função. Então o domínio do função fica
Passo 3
Para a imagem da função vamos ver como fica a função no menor valor do módulo. Sabemos que o menor valor do módulo é em , onde Então o nosso ponto de mínimo global da função será em , ou seja:
Esse será o valor que define o limite inferior da imagem da função. Além disso, a função pode resultar em qualquer outro número, então a imagem da função fica:
Passo 4
Como vimos no passo anterior, a função terá seu mínimo em . Fora isso ela se comportará como uma função módulo que a gente já tá vacinado de tanto plotar. Só fazer duas semirretas que se encontram nesse ponto a vão até o infinito para os dois lados. Desse jeito:
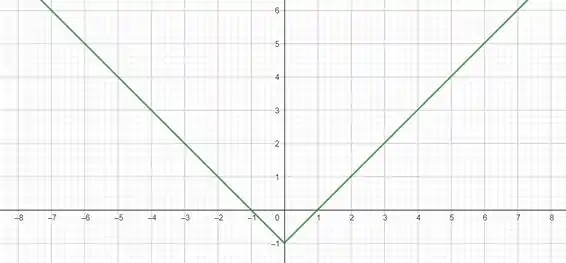
Resposta
Domínio:
Imagem: