Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 71
Ache as equações das retas que passam pela origem e são tangentes a circunferência com centro (2,1) e raio 2.
Passo 1
Faaaaaala galerinha !!
Animados?
Queremos obter as equações das retas que cruzam o ponto (0,0) e tangenciam a circunferência de centro (2,1) e raio 2.
Para começar vamos ilustrar a situação descrita pelo problema.
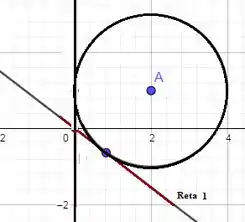
Para obter a equação das retas precisamos de pelo menos um ponto e a sua inclinação. Como já temos o ponto (0,0) precisamos da inclinação, tudo bem?
Passo 2
Boom galera de cowboy, se queremos a equação da reta nós precisamos lembrar como é a sua equação geral, não é?
Então vamos dar uma olhadinha?
E substituindo para o ponto pelos pontos :
A equação da reta também pode ser escrita como:
Onde:
Para nós obtermos a equação da reta que passa por (0,0) nos falta obter a inclinação .
Passo 3
Para calcular a inclinação podemos usar a expressão da distância do centro até a reta tangente, dada por:
Nesta formula os termos e são relativos ao centro do círculo!!
Sabendo que a reta tangência a circunferência:
Substituindo os dados na fórmula:
Elevando ambos os lados ao quadrado para remover a raiz:
Uma vez que descobrimos a inclinação vamos lança-la na fórmula do Passo 1:
Legal, não foi?