Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 10
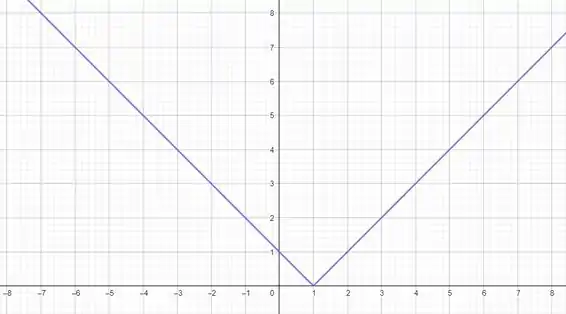
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Vamos fazer uma coisa de cada vez. Primeiro o domínio da nossa função, depois a imagem e por último, vamos determinar o gráfico dela.
Passo 2
A função que temos é um módulo! A função módulo está definida para todo . Então o nosso domínio será todo o conjunto dos números reais:
Passo 3
A nossa imagem será todos os números não negativos! Já que o módulo transforma tudo que se coloca dentro dele em positivo.
Passo 4
O gráfico da função está transladado no eixo em uma unidade! Podemos ver isso da definição de módulo de :
Daqui vemos que serão duas semirretas perpendiculares que se encontram no ponto Dessa forma:
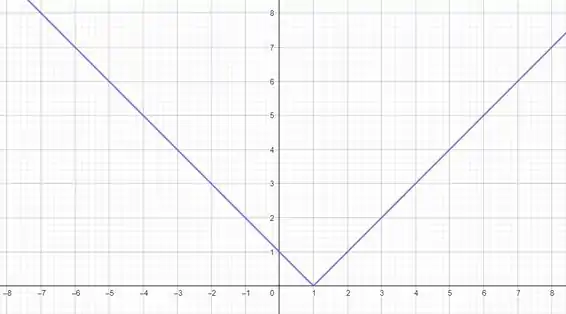
Resposta
Domínio:
Imagem:
Exercícios de Livros Relacionados
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: o ) f x = 1 x 2 ,ep = - 3
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: c ) f x = x 2 ,epq u a l q u e r
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: d ) f x = 2 x + 1 ,ep = 2
Calcule: b )g 0 ,g ( 2 ) e g 2 sendo g x = x x 2 - 1
Simplifique f x - f ( p ) x - p( x ≠ p ) sendo dados: j ) f x = 1 x ,ep = 1