Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 21

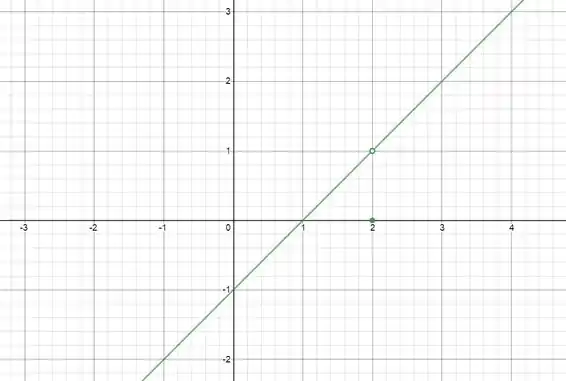
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

f x = 2 x - 1 ,   s e   x ≠ 2 0 ,   s e   x = 2

Passo 1

Vamos começar pelo domínio. Temos que encontrar para que valores de x a função está definida. Ela está definida para todos os reais! A primeira linha exclui o valor da função em x = 2 , mas a segunda linha puxa o 2 de volta pro domínio.

Passo 2

Para qualquer valor de x diferente de 2 , a função se comporta como uma reta, porém tiramos o valor da reta nesse ponto e colocamos o ponto ( 2 ,   0 ) no lugar dele. Daí vamos ter um buraco na nossa reta. No ponto que seria o par ordenado pertencente à reta 2 ,   3 . Ou seja, teremos todos os valores na imagem da função, exceto o valor de y em 3 .

Passo 3

Daí o gráfico da f fica essa reta com um buraco em x = 2 :

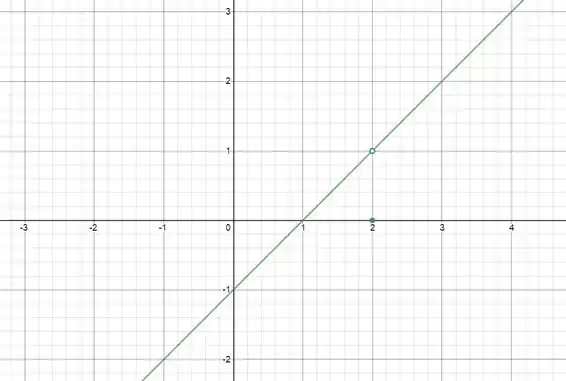
Resposta

Domínio: ( - ∞ ,   + ∞ )

Imagem: { y | y ≠ 3 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se o gráfico da função y=x 2 / 5 é simétrico em relação ao eixo x , à origem ou nenhum dos dois.
Determine se a função y = x c o s x é par, ímpar, ou nenhuma das duas.
Determine o maior intervalo em que a função f ( x ) = ( x + 1 ) 4 é crescente.
Determine se a função y = x 4 + 1 x 3 - 2 x é par, ímpar, ou nenhuma das duas.
Determine (a) o domínio e (b) a imagem de y= 2 s e n ( 3 x + π ) - 1