Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 19
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Antes de tudo, vamos escrever aquele como pra deixar nossa função organizada:
Temos uma função condicional! Na 1ª condição temos uma função constante igual a e na 2ª condição temos uma função constante igual a .
Passo 2
Vamos plotar o gráfico disso:
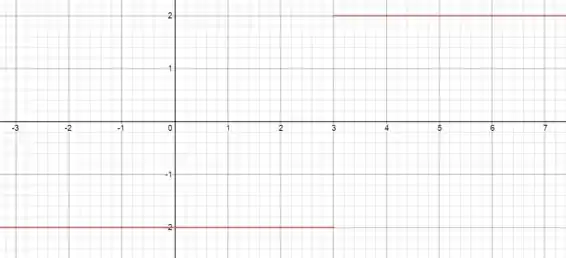
Passo 3
Vemos que a função está definida para qualquer valor de . Então o nosso domínio vai ser . A imagem vai ser e , que são os únicos valores que a função pode assumir.
Resposta
Domínio:
Imagem:
Exercícios de Livros Relacionados
Determine se a função y = x + c o s x é par, ímpar, ou nenhuma das duas.
Determine (a) o domínio e (b) a imagem de y= t g ( 2 x - π )
Suponha que f é uma função ímpar, definida em toda a reta real. A função f ( s e n x ) (se estiver definida) é par?
Expresse o raio de uma esfera em função da área de sua superfície. Em seguida, expresse a área de sua superfície em função do volume.
Determine se o gráfico da função y=x 1 / 5 é simétrico em relação ao eixo x , à origem ou nenhum dos dois.