Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 17
Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.
Passo 1
Essa divisão entre polinômios não está nada amigável para desenhar um gráfico. Vamos tentar simplificar alguma coisa e ficar com uma função mais simples. Lembre que podemos representar uma função quadrática do tipo:
Como
Onde e são as raízes do polinômio. Vamos encontrar essas raízes por bhaskara:
Substituindo os valores do polinômio do numerador:
Daí temos as raízes:
E
Então:
Agora podemos reescrever a com o numerador fatorado bonitinho:
E simplificando:
Nossa não era nada mais do que a equação de uma reta disfarçada! Agora ficou fácil, já sabemos como irá se comportar o domínio, a imagem e o gráfico!
Passo 2
Já sabemos que o domínio e a imagem serão todo o conjunto dos números reais porque a nossa função é um polinômio do 1º grau.
Passo 3
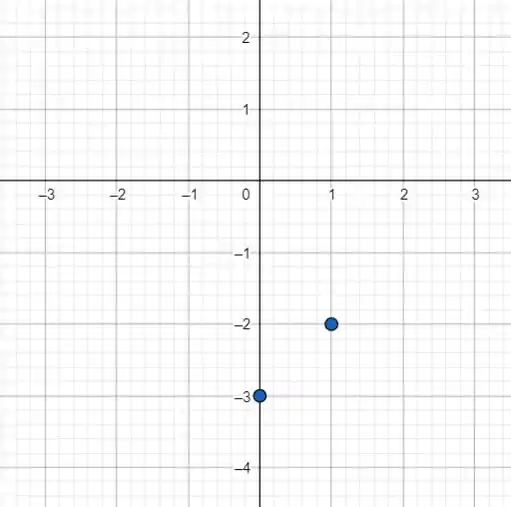
Pra plotar essa função vamos encontrar pontos que satisfaçam a função e depois desenhar a reta que contém esses dois pontos. Vamos fazer e :
Temos os dois pontos pertencentes à reta: e . Plotando esses dois pontos no plano cartesiano:
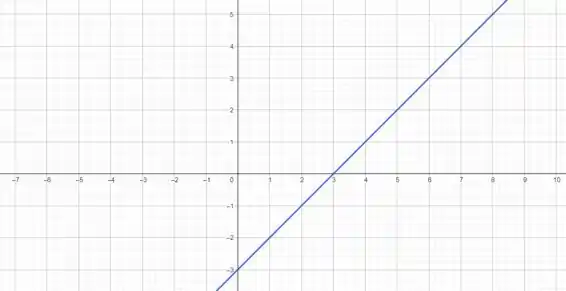
Agora é só desenhar a reta que possui os dois pontos! O gráfico da nossa função é então a reta azul:
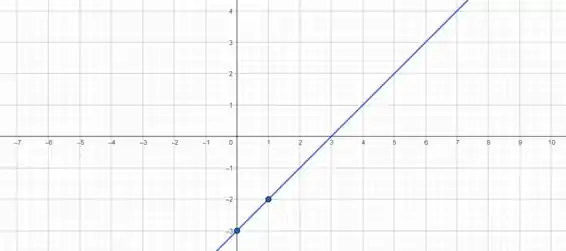
Resposta
Domínio:
Imagem:
